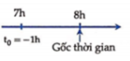
Có hai xe chuyển động ngược chiều nhau. Xe thứ nhất qua a lúc 7 giờ, xe thư hai qua b lúc 7h15'. sau khi qua b được 30ph thì xe thues hai gặp xe thứ nhất ở giữa quãng đường ab. Sau khi gặp nhau xe thứ hai sừng laik nghỉ 10 phút rồi quay về b và gặp xe thứ nhất ở b cách b 10km. tính v của mỗi xe và quãng dường ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
17 tháng 9 2017
Đáp án B
Chọn trục Ox trùng với chiều chuyển động gốc O tại A,
Gốc thời gian là lúc 7h. Sau khoảng thời gian t
- Toạ độ của xe thứ nhất : 
- Toạ độ của xe thứ hai : 
Lúc hai xe gặp nhau thì : 
Vậy hai xe gặp nhau lúc 8h
VT
1 tháng 12 2018
Đáp án C
c, khoảng cách giữa hai xe: 
Suy ra 
hoặc 
Vậy hai xe cách nhau 20km lúc 10h
VT
25 tháng 10 2019
Đáp án B
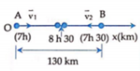
Chọn trục Ox trùng với đường AB, gốc O tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc 7 giờ . Sau thời gian t >0,5h;
- Toạ độ của xe thứ nhất: 
- Toạ độ của xe thứ hai: 
Khi hai xe gặp nhau lúc 8 giờ 30 phút hay t=1,5h
(Dễ thấy với t <0,5h xe thứ nhất không thể gặp xe thứ hai)
DD
7 tháng 8 2016
Cách 1: Theo đề bài thì vận tốc ô tô thứ nhất là AB/(10-7)=AB/3
Vận tốc ô tô thứ 2 là AB/(12-7)=AB/5
Hai ô tô gặp nhau sau khi đi một khoảng thời gian là:
AB: (AB/3+AB/5)= AB:8AB/15= 15/8h = 1h52p30s
=> 2 xe gặp nhau lúc 8h52p30s
Cách 2:
Xe thứ nhất đi từ A đến B trong khoảng thời gian là 10-7=3h=> 1h xe thứ 1 đi được 1/3 đoạn đường AB
Xe thứ 2 đi từ B đến A trong khoảng thời gian là 12-7=5h=> 1h xe thứ 2 đi được 1/5 đoạn đường AB
Từ hai điều trên suy ra, 1h cả 2 xe đi được 1/3+1/5=8/15 đoạn đường AB
Để 2 xe gặp nhau, tức là 2 xe đi tổng quãng đường bằng đúng AB, suy ra, thời gian để hai xe gặp nhau là 1:8/15=15/8h và suy ra đáp án như cách 1
24 tháng 5 2015
Ta có :
1 giờ xe thứ nhất đi đươc \(\frac{1}{2}\) quảng đường AB.
1 giờ xe thứ 2 đi được \(\frac{1}{3}\) quảng đường AB .
1 giờ cả 2 xe đi được \(\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\) quảng đương AB.
Sau 10 phút = \(\frac{1}{6}\) giờ : Xe thứ nhất đi được \(\frac{1}{6}\times\frac{1}{2}=\frac{1}{12}\) quảng đường AB.
Quảng đường còn lại là:
\(1-\frac{1}{12}=\frac{11}{12}\) (của AB)
Thời gian hai xe cùng đi quảng đường còn lại là:
\(\frac{11}{12}\div\frac{5}{6}=\frac{11}{10}\) giờ = 1 giờ 6 phút.
Vậy hai xe gặp nhau lúc 7 giờ 10 phút + 1 giờ 6 phút = 8 giờ 16 phút .
Đáp số : 8 giờ 16 phút
24 tháng 5 2015
Lấy quãng đường AB làm đơn vị quy ước.
Trong 1 giờ xe thứ nhất đi được 1 : 2 = \(\frac{1}{2}\) (quãng đường AB)
Trong 1 giờ xe thứ hai đi được 1 : 3 = \(\frac{1}{3}\) (quãng đường AB)
Xe thứ nhất đi trước xe thứ hai là 7 giờ 10 phút - 7 giờ = 10 phút
Đổi 10 phút = \(\frac{1}{6}\) giờ.
Trong 10 phút xe thứ nhất đi được là \(\frac{1}{2}\times\frac{1}{6}=\frac{1}{12}\) (quãng đường AB)
Quãng đường còn lại hai xe cùng đi là \(1-\frac{1}{12}=\frac{11}{12}\) (quãng đường AB)
Trong một giờ, hai xe cùng đi được \(\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\) (quãng đường AB)
Thời gian để hai xe gặp nhau là : \(\frac{11}{12}:\frac{5}{6}=\frac{11}{10}\)= 1 giờ 6 phút
Thời điểm hai xe gặp nhau là: 7 giờ 10 phút + 1 giờ 6 phút = 8 giờ 16 phút
Đáp số: 8 giờ 16 phút