CMR: x - x2 - 1 < 0 với mọi số thực x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(x-x^2-1=-\left(x^2-x+\frac{1}{4}\right)-\frac{3}{4}=-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\le-\frac{3}{4}< 0\)
Dấu "=" chỉ xảy ra khi:\(\left(x-\frac{1}{2}\right)^2=0\Rightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}\)
Vậy giá trị trên < 0 với mọi số thực x

ta có : \(x-x^2-1=-\left(x^2-x+1\right)=-\left(x^2-2.\dfrac{1}{2}x+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right)\)
\(=-\left(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right)=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
ta có : \(\left(x-\dfrac{1}{2}\right)^2\ge0\) với mọi \(x\) \(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2\le0\) với mọi \(x\)
\(\Leftrightarrow-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le\dfrac{-3}{4}< 0\) với mọi \(x\)
vậy \(x-x^2-1< 0\) với mọi số thực \(x\) (đpcm)

\(-25x^2+5x-1=-\left(25x^2-5x+\dfrac{1}{4}\right)-\dfrac{3}{4}=-\left(5x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}< 0\forall x\)

Ta có :
\(2x-2x^2-3\)
\(=-2\left(x^2-x+\dfrac{3}{2}\right)\)
\(=-2\left(x^2-x+\dfrac{1}{4}+\dfrac{5}{4}\right)\)
\(=-2\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{4}\right]\)
Tới đây ta nhận xét :
\(\left(x-\dfrac{1}{2}\right)^2\ge0\left(\forall x\right)\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{4}\ge\dfrac{5}{4}\left(\forall x\right)\)
Do \(-2\) < 0 nên :
\(-2\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{4}\right]< 0\)
CMR:\(2x-2x^2-1\)<0 Với mọi số thực x.
GIẢI :
\(2x-2x^2-1\)
\(=-2\left(x^2-x+1\right)\)
\(=-2\left(x-2.x.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{4}\right)\)
\(=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\)
Nhận xét : \(\left(x-\dfrac{1}{2}\right)^2\ge0\) với mọi x
\(\Rightarrow-2\left(x-\dfrac{1}{2}\right)^2\le0\) với mọi x
\(\Rightarrow-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}< 0\) với mọi x
Vậy \(2x-2x^2-1< 0\) với mọi x

a) Đề sai thì phải.Phải là CM: \(x^2-x+1>0\) với mọi x
Ta có:
\(x^2-x+1=\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\) nên \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Vậy \(x^2-x+1>0\) với mọi \(x\in R\)
b)Ta có:
\(-x^2+2x-4=-\left(x^2-2x+1\right)-3\)
\(=-\left(x-1\right)^2-3\)
Vì \(-\left(x-1\right)^2\le0\) với mọi x nên \(-\left(x-1\right)^2-3< 0\)
Vậy \(-x^2+2x-4< 0\) với mọi \(x\in R\)

Ta có:
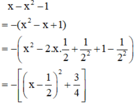
Ta có: 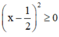 với mọi số thực x
với mọi số thực x
⇒ 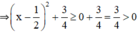 với mọi số thực x
với mọi số thực x
⇒ 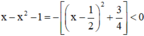 với mọi số thực (ĐPCM)
với mọi số thực (ĐPCM)
\(x-x^2-1\\ =-\left(x^2-x+1\right)\\ =-\left(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\right)\\ =-\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]\\ \left(x-\dfrac{1}{2}\right)^2\ge0\forall x\in R\\ \Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\in R\\ \Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\in R\\ \Rightarrow-\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]< 0\forall x\in R\\ \Leftrightarrow x-x^2-1< 0\forall x\in R\)
Vậy \(x-x^2-1< 0\forall x\in R\)
Ta có: \(x-x^2-1\)
\(=-\left(x^2-x+1\right)\)
\(=-\left(x^2-2x.\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}+1\right)\)
\(=-\left[\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Vì \(-\left(x-\dfrac{1}{2}\right)^2\le0\forall x\in R\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le\dfrac{-3}{4}< 0\forall x\in R\)
-> ĐPCM.