K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
1
Những câu hỏi liên quan
30 tháng 3 2018
drom room có nghĩa sang tiếng việt là phòng ngủ tập thể
chúc
bạn
hok
tốt
nhé
nhớ
k
cho
mình
nha
VT
3 tháng 1 2022
2xy - 3x + 5y=4
2x(y-1) + 5y = 4
2x(y-1) + 5y - 5 = 4 - 5
2x(y-1) - 1(y-1) = -1
(2x-1)(y-1) = -1
Ta thấy -1= (-1).1 => Ta có bảng sau:
| 2x-1 | -1 | 1 |
| y-1 | 1 | -1 |
| x | 0 | 1 |
| y | 2 | 0 |
Như vậy, ta có 2 trường hợp (x;y) thỏa mãn yêu cầu đề bài là ( 0;2 ) ; ( 1;0 )
Hok tốt~
17 tháng 1 2023
11)
\(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^{2^{ }}-4}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^2-2^2}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{\left(x-2\right)\left(x+2\right)}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{x\left(x-3\right)}{2}\)
6 tháng 8 2023
a: \(Q=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{x-4}:\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{x-4}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\cdot\left(-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Khi x=4-2căn 3 thì \(Q=\dfrac{\sqrt{3}-1+2}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}+1}{\sqrt{3}-4}=\dfrac{-7-5\sqrt{3}}{13}\)
c: Q>1/6
=>Q-1/6>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{1}{6}>0\)
=>\(\dfrac{6\sqrt{x}+12-\sqrt{x}+3}{6\left(\sqrt{x}-3\right)}>0\)
=>\(\dfrac{5\sqrt{x}+9}{6\left(\sqrt{x}-3\right)}>0\)
=>căn x-3>0
=>x>9
NN
1
5 tháng 11 2021
Ta có \(\left|7x+5\right|+4\ge4;2\left|7x+5\right|+11\ge11\)
Do đó \(A=\dfrac{2\left|7x+5\right|+11}{\left|7x+5\right|+4}\le\dfrac{11}{4}\)
Vậy GTLN A là \(\dfrac{11}{4}\Leftrightarrow\left|7x+5\right|=0\Leftrightarrow x=-\dfrac{5}{7}\)
LC
20 tháng 9 2018
- Nói mỗi lông hút là một tế bào vì mỗi lông hút đều có những thành phần đặc trưng của 1 tế bào như vách tế bào , màng sinh chất , chất tế bào , nhân , không bào ,.....
- Lông hút không tồn tại mãi , đến một thời gian nào đó nó sẽ rụng và được thay thế bởi một lông hút khác .
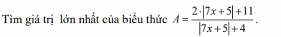
Trả lời:
\(A=\left(1-\frac{x^2-x}{x-1}\right)\left(1+\frac{x^2+x}{x+1}\right)+x^2\) \(\left(ĐKXĐ:x\ne\pm1\right)\)
\(=\frac{x-1-x^2+x}{x-1}.\frac{x+x+x^2+x}{x+1}+x^2\)
\(=\frac{-x^2+2x-1}{x-1}.\frac{x^2+2x+1}{x+1}\)\(+x^2\)
\(=\frac{-\left(x^2-2x+1\right)}{x-1}.\frac{\left(x+1\right)^2}{x+1}+x^2\)
\(=\frac{-\left(x-1\right)^2}{x-1}.\frac{\left(x+1\right)^2}{x+1}+x^2\)
\(=-\left(x-1\right).\left(x+1\right)+x^2\)
\(=-\left(x^2-1\right)+x^2=-x^2+1+x^2=1\)
\(B=\left(2-\frac{x^2-x}{x-1}\right)\left(2+\frac{x^2+x}{x+1}\right)\) \(\left(ĐKXĐ:x\ne\pm1\right)\)
\(=\frac{2x-2-x^2+x}{x-1}.\frac{2x+2+x^2+x}{x+1}\)
\(=\frac{-x^2+3x-2}{x-1}.\frac{x^2+3x+2}{x+1}\)
\(=\frac{-\left(x^2-3x+2\right)}{x-1}.\frac{x^2+3x+2}{x+1}\)
\(=\frac{-\left(x^2-x-2x+2\right)}{x-1}.\frac{x^2+x+2x+2}{x+1}\)
\(=\frac{-\left[x\left(x-1\right)-2\left(x-1\right)\right]}{x-1}.\frac{x\left(x+1\right)+2\left(x+1\right)}{x+1}\)
\(=\frac{-\left(x-1\right)\left(x-2\right)}{x-1}.\frac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(=-\left(x-2\right).\left(x+2\right)=-\left(x^2-4\right)=-x^2+4\)