Chứng minh đẳng thức:
1/n(n+1)=1/n-1/n+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
4 tháng 2 2018
xuất phát từ vế phải và quy đồng mẫu thức, ta có :
VP=\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}\left(dpcm\right)\)
24 tháng 9 2017
Sửa đề:
\(\sqrt{n+1}-\sqrt{n}=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\\ < =>\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)=1\\ < =>n+1-n=1\\ < =>1=1\)(luôn luôn đúng)
=> đfcm
LD
13 tháng 10 2017
biến đổi vế phải ta có :
\(\dfrac{1}{\sqrt{n+1}+\sqrt{n}}=\dfrac{\sqrt{n+1}-\sqrt{n}}{\left(\sqrt{n+1}+\sqrt{n}\right)\left(\sqrt{n+1}-\sqrt{n}\right)}=\sqrt{n+1}-\sqrt{n}\left(đpcm\right)\)
17 tháng 9 2016
\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)+n=2n+1=\left(n+1-n\right)\left(n+1+n\right)=\left(n+1\right)^2-n^2\)
PT
1
CM
17 tháng 6 2019
Ta có:
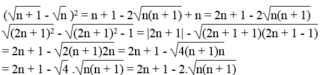
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80
Ta có: \(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
Vì \(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(\Rightarrow\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\left(đpcm\right)\)
Chứng minh
\(\dfrac{1}{n\left(n+1\right)}\)=\(\dfrac{1}{n}-\dfrac{1}{n+1}\)
Ta có:VP=\(\dfrac{1}{n}-\dfrac{1}{n+1}\)=
\(\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}\)
=\(\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}=VT\)(đpcm)