Tìm các số a, b, c, biết rằng : a/2=b/3=c/4 và a2-b2+2c2=108
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
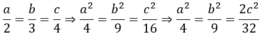
Theo tính chất dãy tỉ số bằng nhau ta có:
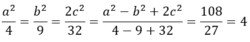
Ta có:
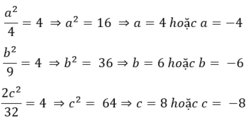
Mà 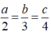 nên a, b và c cùng dấu.
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8

a) \(\dfrac{a}{5}=\dfrac{b}{4}\Rightarrow\dfrac{a^2}{25}=\dfrac{b^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{25}=\dfrac{b^2}{16}=\dfrac{a^2-b^2}{25-16}=\dfrac{1}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{9}\cdot25=\dfrac{25}{9}\\b^2=\dfrac{1}{9}\cdot16=\dfrac{16}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3};b=\dfrac{4}{3}\\a=\dfrac{-5}{3};b=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left(a;b\right)\in\left\{\left(\dfrac{5}{3};\dfrac{4}{3}\right);\left(-\dfrac{5}{3};-\dfrac{4}{3}\right)\right\}\)
b) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=4.4=16\\b^2=4.9=36\\c^2=4,16=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=4;=6;c=8\\a=-4;b=-6;c=-8\end{matrix}\right.\)
Vậy (a;b;c) \(\in\left\{\left(4;6;8\right);\left(-4;-6;-8\right)\right\}\)

Sửa \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\Rightarrow a=2k;b=3k;c=4k\)
\(a^2-b^2+2c^2=108\\ \Rightarrow4k^2-9k^2+32k^2=108\\ \Rightarrow27k^2=108\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4;y=6;z=8\\x=-4;y=-6;z=-8\end{matrix}\right.\)
Ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a^2}{2^2}=\dfrac{b^2}{3^2}=\dfrac{2c^2}{2.4^2}=\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}\)
Áp dụng tcdtsbn , ta có:
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=8\\b=12\\c=16\end{matrix}\right.\)


P≤√a2+2√aab+2b2+√b2+2√2bc+2c2+√c2+2√2ca+2a2P≤a2+2aab+2b2+b2+22bc+2c2+c2+22ca+2a2
P≤√(a+√2b)2+√(b+√2c)2+√(c+√2a)2P≤(a+2b)2+(b+2c)2+(c+2a)2
P≤

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
\(\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{3b^2}{27}=\dfrac{2c^2}{32}=\dfrac{a^2+3b^2-2c^2}{4+27-32}=\dfrac{-16}{-1}=16\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=64\\b^2=144\\c^2=256\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=\pm8\\b=\pm12\\c=\pm16\end{matrix}\right.\)
Vậy \(\left(a;b;c\right)\in\left\{\left(8;12;16\right),\left(-8;-12;-16\right)\right\}\)
Cách khác:
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k\\b=3k\\c=4k\end{matrix}\right.\)
Ta có: \(a^2+3b^2-2c^2=-16\)
\(\Leftrightarrow4k^2+27k^2-32k^2=-16\)
\(\Leftrightarrow k^2=16\)
Trường hợp 1: k=4
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=8\\b=3k=12\\c=4k=16\end{matrix}\right.\)
Trường hợp 2: k=-4
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=-8\\b=3k=-12\\c=4k=-16\end{matrix}\right.\)

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

tham khảo!!
https://lazi.vn/edu/exercise/tim-cac-so-a-b-c-biet-rang-a-2-b-3-c-4-va-a-2-b-2-2c-2-108
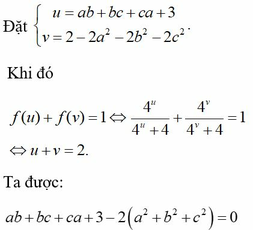
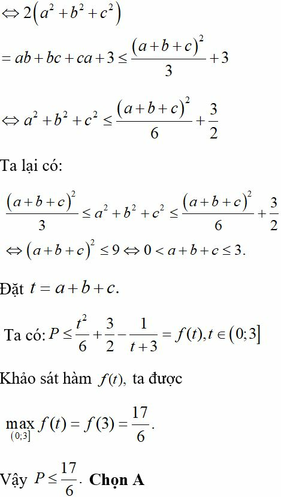
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}\)
Theo t/c dãy tỉ số bằng nhau có:
\(\frac{a^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)
=>\(\frac{a^2}{4}=4\Rightarrow a^2=4.4=16=4^2=\left(-4\right)^2\Rightarrow a=\)+4
=>\(\frac{b^2}{9}=4\Rightarrow b^2=4.9=36=6^2=\left(-6\right)^2\Rightarrow b=\)+6
=>\(\frac{2c^2}{32}=4\Rightarrow c^2=4.32:2=64=8^2=\left(-8\right)^2\Rightarrow c=\)+8
Vậy ta có 2 cặp (a,b,c) là: (4,6,8) và (-4,-6,-8).
Ban vao cau hoi tuong tu nha Nguyễn Thị Thanh Hà