trên hình bên có mấy hình tam giác hãy kể tên các tam giác đó:
...
Đọc tiếp
trên hình bên có mấy hình tam giác hãy kể tên các tam giác đó:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 4 2018
Các tam giác cân trên hình 112:
-ΔADE cân tại A: có các cạnh bên là AD và AE; cạnh đáy: DE; góc D và góc E là hai góc ở đáy; góc A là góc ở đỉnh
-ΔABC cân tại A: có các cạnh bên là AB và AC; cạnh đáy: BC; góc B và góc C là hai góc ở đáy; góc A là góc ở đỉnh
-ΔAHC cân tại A: có các cạnh bên là AH và AC; cạnh đáy: HC; góc H và góc C là hai góc ở đáy; góc A là góc ở đỉnh
CM
25 tháng 5 2017
Từ giả thiết và tính chất về góc của tam giác vuông BCD ta có:
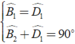
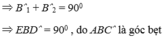
Vậy trong hình vẽ có 3 tam giác vuông là ABE, BCD, EDB
CM
9 tháng 11 2017
Có tất cả 16 hình tam giác. Các tam giác có cạnh AG là: ∆AGB, ∆AGP, ∆AGN, ∆AGC.
CM
7 tháng 1 2018
Có tất cả 16 hình tam giác. Các tam giác có cạnh AG là: Δ AGB, Δ AGP, Δ AGN, Δ AGC.
CM
7 tháng 11 2017
a. Trong hình có 2 cặp cạnh song song. Đó là: AB song song với CD và AD song song với BC
b. Ba cặp cạnh vuông góc với nhau là: AB vuông góc với AD; AB vuông góc với BC và BC vuông góc với CD
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta thấy: \(\Delta MEF\)cân tại M do ME = MF có:
+ cạnh bên: ME, MF
+ cạnh đáy: EF
+ góc ở đỉnh: \(\widehat {EMF}\)
+ góc ở đáy: \(\widehat {MEF}\),\(\widehat {MFE}\)
\(\Delta MNP\) cân tại M do MN = MP có:
+ cạnh bên: MN, MP
+ cạnh đáy: NP
+ góc ở đỉnh: \(\widehat {NMP}\)
+ góc ở đáy: \(\widehat {NPM}\), \(\widehat {PNM}\)
\(\Delta MHP\) cân tại M do MH = MP có:
+ cạnh bên : MH, MP
+ cạnh đáy: HP
+ góc ở đỉnh: \(\widehat {PMH}\)
+ góc ở đáy: \(\widehat {MPH}\),\(\widehat {MHP}\)
PT
1
CM
10 tháng 6 2018
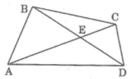
Ta có 8 tam giác: ΔABC, ΔABD, ΔBCD, ΔACD, ΔBCE, ΔABE, ΔADE, ΔCDE
6 tam giác
\(\Delta ABM\) ; \(\Delta AMN\) ; \(\Delta ANC\) ; \(\Delta ABN\) ; \(\Delta AMC\) ; \(\Delta ABC\)
hình bên có 6 hình tam giác đó là
tam giác ABM; tam giác AMN; tam giác ANC; tam giác ABN; tam giác AMC; tam giác ABC