cho hình vuông ABCD , gọi M là trung điểm AB . Tính góc AMC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tự vẽ hình nhá :))
*Nối MC
Số đo cạnh AM là : 12 : 2 = 6 (dm)
Vì 12 dm2 = 1 x 12 mà nửa AB đã là 6 dm => Chiều dài = 12,chiều rộng là 1
Diện tích hình tam giác AMC là : 6 x 1 : 2 = 3 dm2
Đ/s :....
( Mình ko chắc lắm )
Vì diện tích hình chữ nhật ABCD là 12dm2 nên thoả mãn điều kiện chiều dài là 3dm, chiều rộng là 4dm.
Vậy độ dài đáy hình tam giác AMC là:
4: 2 = 2 (dm)
Diện tích hình tam giác AMC là: 2* 3/2= 3 (dm2)
Đ/s: 3dm2

a: Xét ΔBAC có BN/BA=BM/BC=1/2
nên MN//AC
=>MN vuông góc AB
b: ΔBAC vuông tại A
mà AM là trung tuyến
nên MA=MC
c: Xét tứ giác AMBD có
N là trung điểm chung của AB và MD
MA=MB
=>AMBD là hình thoi

Chọn D
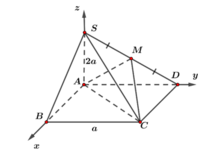
Để thuận tiện trong việc tính toán ta chọn a = 1.
Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A, tia Ox chứa đoạn thẳng AB, tia Oy chứa đoạn thẳng AD, tia Oz chứa đoạn thẳng AS. Khi đó: A(0;0;0), B(1;0;0), C(1;1;0), S(0;0;2), D(0;1;0)
Vì M là trung điểm SD nên tọa độ là M 0 ; 1 2 ; 1
Ta có
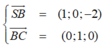
![]()
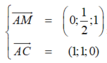
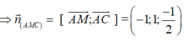
Gọi α là góc giữa hai mặt phẳng (AMC) và (SBC).
Suy ra
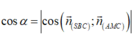
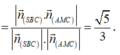
Mặt khác
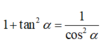
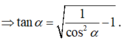
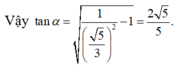

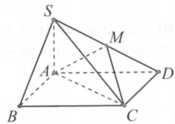
Gọi O là tâm đáy \(\Rightarrow OD\perp AC\) (đường chéo hình vuông)
Gọi N là trung điểm AD \(\Rightarrow\) MN là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}SA=\dfrac{a\sqrt{5}}{2}\\MN||SA\end{matrix}\right.\)
Do \(SA\perp\left(ABCD\right)\Rightarrow MN\perp\left(ABCD\right)\Rightarrow MN\perp AC\)
Gọi P là trung điểm AO \(\Rightarrow\) NP là đường trung bình tam giác OAD
\(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}OD=\dfrac{a\sqrt[]{2}}{4}\\NP||OD\end{matrix}\right.\)
Mà \(OD\perp AC\Rightarrow NP\perp AC\)
\(\Rightarrow AC\perp\left(MNP\right)\)
Lại có AC là giao tuyến (AMC) và (ABCD)
\(\Rightarrow\widehat{MPN}\) là góc giữa (AMC) và (ABCD)
\(tan\widehat{MPN}=\dfrac{MN}{NP}=\sqrt{10}\Rightarrow\widehat{MPN}\approx72^027'\)
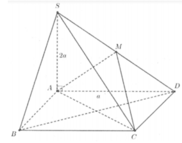



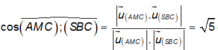
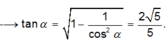
\(\widehat{AMC}\simeq117^0\)