X4 - 4x3 - 7x2 +16x -3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Lời giải:
$A=x^4-4x^3+7x^2-12x+75$
$=(x^2-2x)^2+3x^2-12x+75$
$=(x^2-2x)^2+3(x^2-4x+4)+63$
$=(x^2-2x)^2+3(x-2)^2+63\geq 63$
Vậy $A_{\min}=63$. Giá trị này đạt tại $x^2-2x=x-2=0$
$\Leftrightarrow x=2$
NK
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
\(A=\left(x^4-4x^3+4x^2\right)+\left(3x^2-12x+12\right)+63\)
\(A=x^2\left(x^2-4x+4\right)+3\left(x^2-4x+4\right)+63\)
\(A=\left(x^2+3\right)\left(x-2\right)^2+63\ge63\)
\(A_{min}=63\) khi \(x=2\)
CM
22 tháng 1 2017
Ta có x 4 – 4 x 3 + 8 x 2 – 16 x + 16 = 0 ⇔ ( x 4 + 8 x 2 + 16 ) – ( 4 x 3 + 16 x ) = 0 ⇔ x 2 + 4 2 - 4 x x 2 + 4 = 0 ⇔ x 2 + 4 x 2 + 4 - 4 x = 0 ⇔ x 2 + 4 x - 2 2 = 0
ó x = 2
Vậy x 0 = 2
Đáp án cần chọn là: B
L
1
H
1
5 tháng 3 2023
P(x)+Q(x)-R(x)
=-5x^3+7x^2-2x+8+4x^3-7x+3-6x^3-4
=-7x^3+7x^2-9x+7
HQ
13 tháng 7 2019
Giải phương trình??? sử dụng Hooc-ne cho nhanh nhá :v
1) \(x^4-8x^2+4x+3=0\)
( dùng máy tính ta đoán được 1 nghiệm chính xác là -3 )
3 1 0 -8 4 3 1 -3 1 1 0
\(\Leftrightarrow\left(x+3\right)\left(x^3-3x^2+x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^3-3x^2+x+1=0\left(2\right)\end{matrix}\right.\)
Tiếp tục dùng máy tính ta tìm được 1 nghiệm chính xác của pt ( 2 ) là 1
1 1 -3 1 1 1 -2 -1 0
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x^2-2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-1=0\\x^2-2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\\x=1+\sqrt{2}\\x=1-\sqrt{2}\end{matrix}\right.\)
rồi mấy câu còn lại tương tự
CM
17 tháng 5 2018
a) ( x 2 – 4x + 1)( x 2 – 2x + 3).
b) ( x 2 + 5x – 1)( x 2 + x – 1).
CM
26 tháng 6 2018
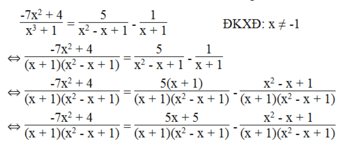
⇔ -7 x 2 + 4 = 5x + 5 – x 2 + x – 1
⇔ -7 x 2 + x 2 – 5x – x = 5 – 1 – 4
⇔ -6 x 2 – 6x = 0
⇔ - x 2 – x = 0
⇔ x(x + 1) = 0
⇔ x = 0 hoặc x + 1 = 0
⇔ x = 0 hoặc x = -1 (loại)
Vậy phương trình có nghiệm x = 0.
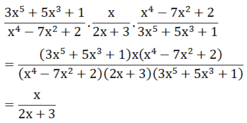
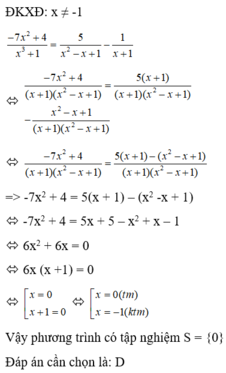
Dùng pp hệ số bất định nha bạn
Đặt
A = \(x^4-4x^3-7x^2+16x-3\)
A \(=\left(x^2+ax+1\right)\left(x^2+bx-3\right)\)
A \(=x^4+ax^3+x^2+bx^3+abx^2+bx-3x^2-3ax-3\)
A \(=x^4+\left(a+b\right)x^3+\left(1+ab-3\right)x^2+\left(b-3a\right)x-3\)
Đồng nhất 2 đa thức ta được :
\(\left\{{}\begin{matrix}a+b=-4\\-2+ab=-7\\b-3a=16\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=-5\\b=1\end{matrix}\right.\)
\(\Rightarrow A=\left(x^2-5x+1\right)\left(x^2+x-3\right)\)