ptrinh :x2-2(m+1)x-3=0
tìm m để phương trình có nghiệm kép
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2022
1: \(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-m+1\right)\)
=1+4m-4
=4m-3
Để phương trình có nghiệm kép thì 4m-3=0
hay m=3/4
Thay m=3/4 vào pt, ta được: \(x^2-x+\dfrac{1}{4}=0\)
hay x=1/2
2: Để phương trình có hai nghiệm thì 4m-3>=0
hay m>=3/4
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}2x_1+x_2=5\\x_1+x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-3\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=-m+1\)
=>1-m=-12
hay m=13
3 tháng 6 2017
phương trình có
\(\Delta^'=\left(m+3\right)^2-m^2-3=m^2+6m+9-m^2-3\)
\(=6m+6\)
- phương trình có nghieemk kép \(\Leftrightarrow\Delta^'=0\Leftrightarrow6m+6=0\Leftrightarrow m=-1\)
- phương trình có hai nghiệm phân biệt \(\Leftrightarrow\Delta^'>0\Leftrightarrow6m+6>0\Leftrightarrow m>-1\)áp dụng viet : \(\hept{\begin{cases}x_1+x_2=-2\left(m+3\right)\\x_1.x_2=m^2+3\end{cases}}\)theo giả thiêt có \(x_1-x_2=2\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4\)
\(\Leftrightarrow4\left(m+3\right)^2-4\left(m^2+3\right)=4\Leftrightarrow m^2+6m+9-m^2-3=1\)\(\Leftrightarrow6m=-5\Leftrightarrow m=-\frac{5}{6}\left(tmdk\right)\)
25 tháng 1 2023
a: Thay x=-1 vào (6), ta được:
1+2m+m+6=0
=>3m+7=0
=>m=-7/3
x1+x2=-2m/1=-2*7/3=-14/3
=>x2=-14/3-x1=-14/3+1=-11/3
b: \(\text{Δ}=0^2-2\left(2m+m+6\right)=-2\left(3m+6\right)\)
Để phương trình có nghiệm kép thì 3m+6=0
=>m=-2
Khi m=-2 thì (6) sẽ là x^2+2*(-2)-2+6=0
=>x^2-4x+4=0
=>x=2
29 tháng 1 2023
ụa bạn ơi, trên câu a á m= -7/3 vậy sao xuống dưới thành 7/3 rồi
27 tháng 2 2021
Bạn giải denta và chú ý điều kiện của a nhá
Y
30 tháng 3 2023
\(a,\)Để pt \(x^2+\left(2m+1\right)x+m\left(m-1\right)=0\) có nghiệm kép thì \(\Delta=0\)
\(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-m\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+4m=0\)
\(\Leftrightarrow8m+1=0\)
\(\Leftrightarrow m=-\dfrac{1}{8}\)
Thay \(m=-\dfrac{1}{8}\) vào pt
\(\Rightarrow x^2+\left[2.\left(-\dfrac{1}{8}\right)+1\right]x-\dfrac{1}{8}\left(-\dfrac{1}{8}-1\right)=0\)
\(\Rightarrow x^2+\dfrac{3}{4}x+\dfrac{9}{64}=0\)
\(\Rightarrow x=-\dfrac{3}{8}\)
\(b,\) Thay \(m=1\) vào pt :
\(\Rightarrow x^2+\left(2.1+1\right)x+1\left(1-1\right)=0\)
\(\Rightarrow x^2+3x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
23 tháng 4 2023
Để phương trình có nghiệm kép thì 6^2-4(m-2)=0
=>4(m-2)=36
=>m-2=9
=>m=11
=>x^2+6x+9=0
=>x=-3
CM
12 tháng 7 2017
Phương trình m x 2 – 2(m – 1)x + 2 = 0 có nghiệm kép khi và chỉ khi m ≠ 0 và Δ = 0
Ta có: ∆ = - 2 m - 1 2 – 4.m.2 = 4( m 2 – 2m + 1) – 8m
= 4( m 2 – 4m + 1)
∆ = 0 ⇔ 4( m 2 – 4m + 1) = 0 ⇔ m 2 – 4m + 1 = 0
Giải phương trình m 2 – 4m + 1 = 0. Ta có:
∆ m = - 4 2 – 4.1.1 = 16 – 4 = 12 > 0
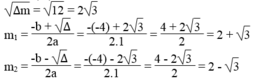
Vậy với m = 2 + 3 hoặc m = 2 - 3 thì phương trình đã cho có nghiệm kép.
CM
31 tháng 10 2018
Phương trình 3 x 2 + (m + 1)x + 4 = 0 có nghiệm kép khi và chỉ khi ∆ = 0
Ta có : ∆ = m + 1 2 – 4.3.4 = m 2 + 2m + 1 – 48 = m 2 + 2m – 47
∆ = 0 ⇔ m 2 + 2m – 47 = 0
Giải phương trình m 2 + 2m – 47 = 0. Ta có:
∆ m = 2 2 – 4.1.(-47) = 4 + 188 = 192 > 0
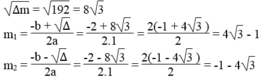
Vậy với m = 4 3 – 1 hoặc m = -1 - 4 3 thì phương trình đã cho có nghiệm kép.
26 tháng 4 2020
A, ta có: \(\Delta’\)=m2-1
Vậy trình có 2 nghiệm phân biệt <=> m2-1>0 => m>1
B,Phương trình có nghiệm kép khi: m2-1=0 => m=+- 1
Nghiem kép đó là: 0
26 tháng 4 2020
\(x^2+2\left(m+1\right)x+2m+2=0\)
\(\Delta'=\left(m+1\right)^2-\left(2m+2\right)=m^2-1\)
a, Để phương trình có hai nghiệm phân biệt thì:
\(\Delta'>0\)
\(\Leftrightarrow m^2>1\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow m< -1;m>1\)
b, Phương trinh có nghiệm kép khi:
\(\Delta'\ge0\)
\(\Leftrightarrow m^2-1\ge0\)
\(\Leftrightarrow m\le-1;m\ge1\)
Theo Viet ta có:
\(x_1+x_2=-2\left(m+1\right)\)
\(x_1x_2=2\left(m+1\right)\)
\(x_1^2+x_2^2=8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\)
\(\Leftrightarrow4m^2+4m-8=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=1\\m=-2\end{cases}}\)
So với điều kiện phương trình có nghiệm m=1 ; m =-2
LA
3 tháng 5 2022
1.
xét delta có
25 -4(-m-3)
= 25 + 4m + 12
= 4m + 37
để phương trình có nghiệm kép thì delta = 0
=> 4m + 37 = 0 => m = \(\dfrac{-37}{4}\)
2.
a) xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có nghiệm kép thì delta = 0
=> -4m + 37 = 0
=> m = \(\dfrac{37}{4}\)
b)
xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có 2 nghiệm phân biệt thì delta > 0
=> -4m + 37 > 0
=> m < \(\dfrac{37}{4}\)
\(\Delta'=\left[-\left(m+1\right)\right]^2-1\cdot\left(-3\right)\)
\(=m^2+2m+1+3\\ =m^2+2m+4\)
Để pt có nghiệm kép \(\Leftrightarrow\Delta'=0\\ \Leftrightarrow m^2+2m+4=0\) (1)
\(\Delta'_m=1^2-1\cdot4=1-4=-3\)
Vì \(\Delta'< 0\) nên pt (1) vô nghiệm
Vậy ko có giá trị nào của m để pt đã cho có nghiệm kép