Giúp min
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C1
0
TH
0
TH
0
TD
0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
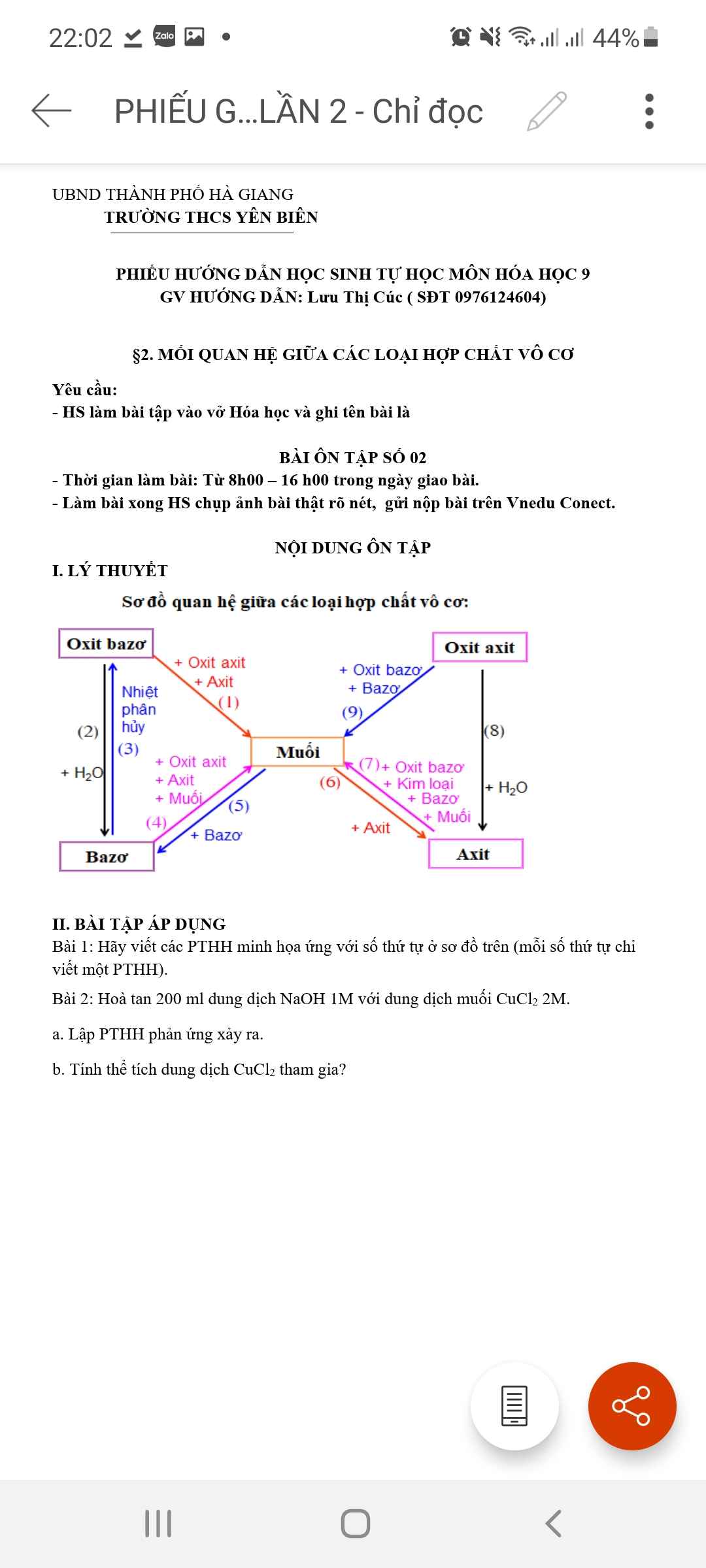
\(C=\dfrac{-1}{\left(x-6\sqrt{x}+9\right)+1}=\dfrac{-1}{\left(\sqrt{x}-3\right)^2+1}\ge\dfrac{-1}{1}=-1\)
\(C_{min}=-1\) khi \(x=9\)
\(E=\dfrac{2}{-4-\left(x-2\sqrt{x}+1\right)}=\dfrac{2}{-4-\left(\sqrt{x}-1\right)^2}\ge\dfrac{2}{-4}=-\dfrac{1}{2}\)
\(E_{min}=-\dfrac{1}{2}\) khi \(x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
\(B=\dfrac{2}{-1-\left(x-4\sqrt{x}+4\right)}=\dfrac{2}{-1-\left(\sqrt{x}-2\right)^2}\ge\dfrac{2}{-1}=-2\)
\(B_{min}=-2\) khi \(x=4\)
\(D=\dfrac{-3}{x+8\sqrt{x}+20}\ge-\dfrac{3}{20}\)
\(D_{min}=-\dfrac{3}{20}\) khi \(x=0\)
9 tháng 9 2021
\(A=\dfrac{2}{4\sqrt{x}-x-5}=\dfrac{2}{-\left(x-4\sqrt{x}+4+1\right)}=\dfrac{2}{-\left(\sqrt{x}-2\right)^2-1}\)
\(-\left(\sqrt{x}-2\right)^2-1\le-1\\ \Leftrightarrow\dfrac{2}{-\left(\sqrt{x}-2\right)^2-1}\ge-2\)
Dấu \("="\Leftrightarrow x=4\)
\(B=\dfrac{-3}{x+8\sqrt{x}+20}=\dfrac{-3}{\left(\sqrt{x}+4\right)^2+4}\)
\(\left(\sqrt{x}+4\right)^2+4\ge4\\ \Leftrightarrow\dfrac{3}{\left(\sqrt{x}+4\right)^2+4}\le\dfrac{3}{4}\\ \Leftrightarrow\dfrac{-3}{\left(\sqrt{x}+4\right)^2+4}\ge-\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\sqrt{x}+4=0\Leftrightarrow x\in\varnothing\)
Vậy dấu \("="\) không xảy ra
N
13 tháng 11 2021
Bài 1:
a. \(Q=A=UIt=220\left(\dfrac{1000}{220}\right)\cdot1=1000\left(J\right)\)
b. \(A'=Pt=1000\cdot3\cdot30=90000\)Wh = 90kWh
\(\Rightarrow T=A'\cdot1000=90\cdot1000=90000\left(dong\right)\)
13 tháng 11 2021
Bài 1.
Điện trở bếp: \(R_b=\dfrac{U_b^2}{P_b}=\dfrac{220^2}{1000}=48,4\Omega\)
Dòng điện qua bếp: \(I_b=\dfrac{P_b}{U_b}=\dfrac{1000}{220}=\dfrac{50}{11}A\)
Nhiệt lượng bếp tỏa ra trong 1s:
\(Q=RI^2=48,4\cdot\left(\dfrac{50}{11}\right)^2\cdot1=1000J\)
Điện năng tiêu thụ của bếp trong 1 tháng:
\(A=UIt=220\cdot\dfrac{50}{11}\cdot30\cdot3\cdot3600=324000000J=90kWh\)
Tiền phải trả:
\(T=90\cdot1000=90000\left(đồng\right)\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 6 2023
4\(\times\)7\(\times\)25\(\times\)3
= (4 \(\times\) 25) \(\times\) (7 \(\times\) 3)
= 100 \(\times\) 21
= 2 100
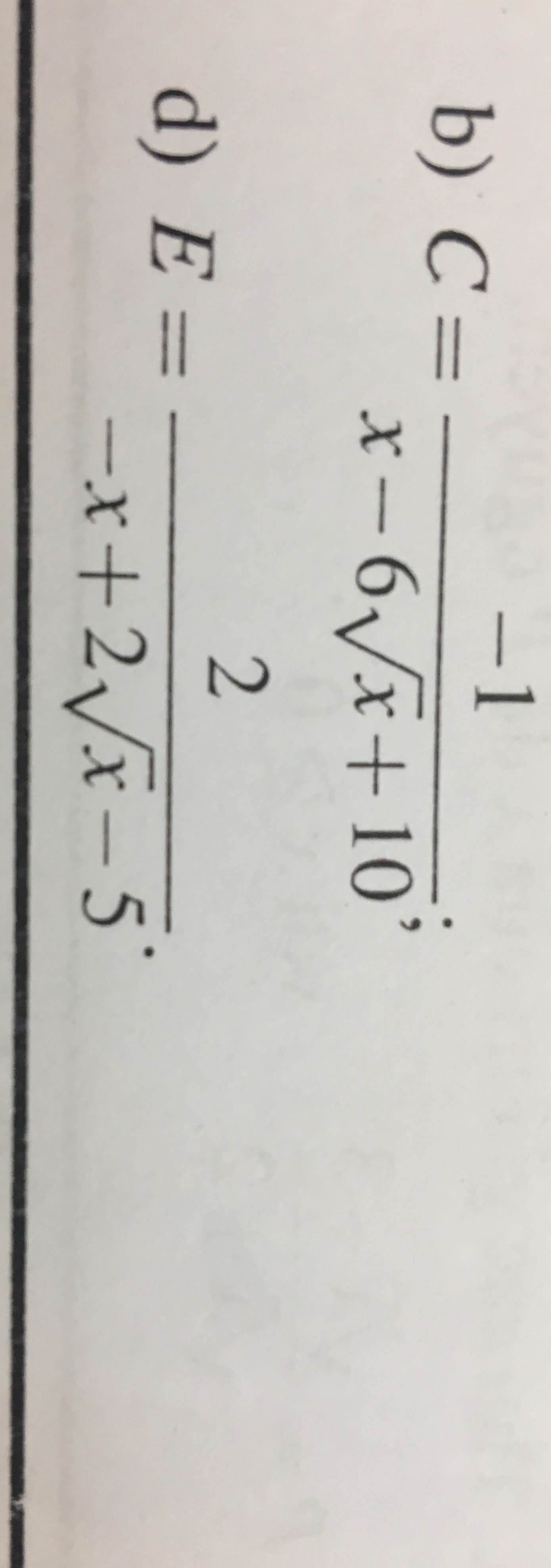
Hình đầu bị ngược kìa bạn ơi