O2VÀ CD2 LÀ GÌ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
29 tháng 9 2019
Ta có: Hai góc ∠O2và ∠O4là hai góc đối đỉnh vì mỗi cạnh góc ∠O1là tia đối của một cạnh ∠O4 và ngược lại
SR
2
MN
6 tháng 5 2021
\(3Fe+2O_2\underrightarrow{^{t^0}}Fe_3O_4\)
\(4Al+3O_2\underrightarrow{^{t^0}}2Al_2O_3\)
17 tháng 11 2023
a: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
Xét tứ giác OCAD có
H là trung điểm chung của OA và CD
Do đó: OCAD là hình bình hành
Hình bình hành OCAD có OC=OD
nên OCAD là hình thoi
b: Xét ΔOAC có OC=CA=OA=R
nên ΔOAC đều
=>\(\widehat{CAO}=60^0\)
Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}+60^0=90^0\)
=>\(\widehat{CBA}=30^0\)
Xét ΔBDC có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBDC cân tại B
ΔBDC cân tại B
mà BH là đường cao
nên BH là phân giác của góc CBD
=>\(\widehat{CBD}=2\cdot\widehat{CBH}=60^0\)
Xét ΔBCD cân tại B có \(\widehat{CBD}=60^0\)
nên ΔBCD đều
c: BO=OA
OA=2OH
Do đó: BO=2OH
=>BO/BH=2/3
Xét ΔCDB có
BH là đường trung tuyến
\(BO=\dfrac{2}{3}BH\)
Do đó: O là trọng tâm của ΔCDB
Xét ΔCDB có
O là trọng tâm
M là trung điểm của BC
Do đó: D,O,M thẳng hàng
d: Xét ΔCAB vuông tại C có CH là đường cao
nên \(AH\cdot HB=CH^2\)
=>\(4\cdot AH\cdot HB=4\cdot CH^2=\left(2CH\right)^2=CD^2\)
10 tháng 4 2023
a, - Dẫn từng khí qua Ca(OH)2 dư.
+ Có tủa trắng: CO2
PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng: CH4, C2H4, C2H2. (1)
- Dẫn khí nhóm (1) qua dd AgNO3/NH3.
+ Xuất hiện tủa vàng: C2H2.
PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)
+ Không hiện tượng: CH4, C2H4. (2)
- Dẫn khí nhóm (2) qua dd brom dư.
+ Dd nhạt màu dần: C2H4.
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: CH4.
b, - Dẫn từng khí qua dd Ca(OH)2
+ Xuất hiện tủa trắng: CO2
PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng: CH4, C2H2 và O2. (1)
- Dẫn khí nhóm (1) qua dd AgNO3/NH3.
+ Có tủa vàng: C2H2.
PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)
+ Không hiện tượng: CH4 và O2. (2)
- Cho tàn đóm đỏ vào 2 khí nhóm (2)
+ Que đóm bùng cháy: O2.
+ Không hiện tượng: CH4.
c, - Dẫn từng khí qua dd Ca(OH)2.
+ Có tủa trắng: SO2, CO2 (1)
PT: \(SO_2+Ca\left(OH\right)_2\rightarrow CaSO_3+H_2O\)
\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng: C2H2, CH4 và C2H4. (2)
- Dẫn khí nhóm (1) qua dd nước brom dư.
+ Dd nhạt màu dần: SO2
PT: \(SO_2+Br_2+2H_2O\rightarrow2HBr+H_2SO_4\)
+ Không hiện tượng: CO2.
- Dẫn khí nhóm (2) qua dd AgNO3/NH3
+ Có tủa vàng: C2H2.
PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)
+ Không hiện tượng: CH4, C2H4 (3)
- Dẫn khí nhóm (3) qua dd brom dư.
+ Dd nhạt màu dần: C2H4
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: CH4.
16 tháng 8 2021
O A B C D H M
a, xét tam giác CHA và tg CHO có : CH chung
AH = HO do H là trđ của AO (gt)
^CHA = ^CHO = 90
=> tg CHA = tg CHO (2cgv)
=> CH = CO
có AB _|_ CD => A là điểm chính giữa của cung CD => AC = AD mà OC = OD
=> AC = CO = OD = DA
=> ACOD là hình thoi
b, C thuộc đường tròn đường kính AB => ^ACB = 90 => AC _|_ CB
có AC // DO do ACOD là hình thoi
=> DO _|_ CB
M là trung điểm của dây BC (Gt) => OM _|_ BC (định lí)
=> D;O;M thẳng hàng
c, xét tg ACB có ^ACB = 90 và CH _|_ AB
=> AH.HB = CH^2
=> 4AH.HB = 4CH^2
=> 4AH.HB = (2CH)^2
mà 2CH = CD
=> CD^2 = 4AH.HB
CM
25 tháng 5 2017
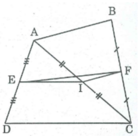
Với 3 điểm E,I,F bất kì ta có: EF ≤ EI + IF (dấu “ = ” xảy ra khi I nằm giữa E và F) mà EI = CD / 2 ; IF= AB / 2 (chứng minh trên)
⇒ E F ≤ C D 2 + A B 2
Vậy E F ≤ A B + C D 2 (dấu bằng xảy ra khi AB // CD)
8 tháng 6 2023
\(KCN->K^++CN^-\\ Cd\left(NO_3\right)_2->Cd^{2+}+2NO_3^-\\ Cd^{2+}+CN^-⇌\left[Cd\left(CN\right)\right]^+\\ \left[Cd\left(CN\right)\right]^++CN^-⇌\left[Cd\left(CN\right)_2\right]\\ \left[Cd\left(CN\right)_2\right]+CN^-⇌\left[Cd\left(CN\right)_3\right]^-\\ \left[Cd\left(CN\right)_3\right]^-+CN^-⇌\left[Cd\left(CN\right)_4\right]^{2-}\)
NQ
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)
CO2 là khí cacbônic
O2 là khí ô xi
O2 là viết tắt của khí ôxi
CO2 là viết tắt của khí cacbônic