Giải phương trình : x6 - 7x3 - 8 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
NT
0
PT
1
CM
5 tháng 10 2017
Đặt t = x 3 thì phương trình x 6 + 2003 x 3 - 2005 = 0 trở thành
t 2 + 2003 t - 2005 = 0
Vì 1 . - 2005 < 0 suy ra phương trình ẩn t có 2 nghiệm trái dấu
Suy ra có phương trình đã cho có một nghiệm âm.
Đáp án cần chọn là: B
CM
15 tháng 1 2019
Chọn đáp án B
Phương trình đã cho tương đương với:
Xét hàm số f t = t 3 + 3 t trên ℝ
Tacó f ' t = 3 t 2 + 3 > 0 , ∀ t ∈ ℝ nên hàm số f t đồng biến trên ℝ
Suy ra
Xét hàm số g x = x + 1 x trên 1 2 ; 2
Ta có g ' x = 1 - 1 x 2
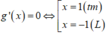
Bảng biến thiên:
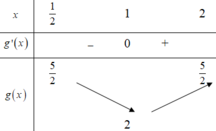
Dựa vào bảng biến thiên, để phương trình đã cho có hai nghiệm phân biệt trên 1 2 ; 2
⇔ Đường thẳng y = m cắt đồ thị hàm số g x = x + 1 x tại hai điểm phân biệt trên 1 2 ; 2
⇔ 2 < m ≤ 5 2
CM
4 tháng 11 2018
Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
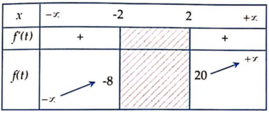
Bảng biến thiên:
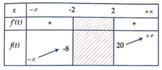
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.
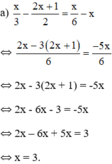
x6 - 7x3 - 8 = 0
\(\Leftrightarrow\left(x^3+1\right)\left(x^3-8\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)\left(x-2\right)\left(x^2+2x+4\right)=0\left(1\right)\)Do \(x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) và \(x^2+2x+4=\left(x+1\right)^2+3>0\) với mọi x
Nên (1) \(\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\Leftrightarrow x\in\left\{-1;2\right\}\)
\(\left(x^3-1\right)\left(x^3+8\right)=0\)
\(\left\{{}\begin{matrix}x^3-1=0\Rightarrow x=1\\x^3+8=0\Rightarrow x=-2\end{matrix}\right.\)