Tổng các nghiệm của phương trình:
(x2 + 4x - 1)2 - 3(x2 + 4x) - 1 = 0 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 1 2019
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = x + 3 ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = 1; x2 = 3
x1 có thỏa mãn điều kiện nói trên
x2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
CM
12 tháng 12 2017
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = x + 3 ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = 1 ; x 2 = 3
x 1 có thỏa mãn điều kiện nói trên
x 2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
CM
15 tháng 4 2018
Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
17 tháng 2 2021
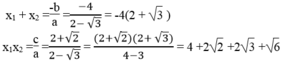
a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)
Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2
nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì
\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau
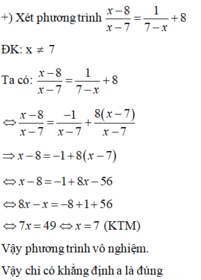
Đáp số nhanh: với cách giải nhanh: S=-8
chi tiết đáp số chậm
với cách giải chậm
\(x^2+4x-1=t\)
\(\left(t\right)^2-3\left(t+1\right)-1=0\)
\(t^2-3t-4=0\)
\(\left[{}\begin{matrix}t=-1\\t=4\end{matrix}\right.\)
\(t=-1\Rightarrow x\left(x+4\right)=0\Rightarrow\left[{}\begin{matrix}x_1=0\\x_2=-4\end{matrix}\right.\)
\(t=4\Rightarrow\left(x-1\right)\left(x+5\right)\left[{}\begin{matrix}x_3=1\\x_4=-5\end{matrix}\right.\)
S=0-4+1-5=-8
Đặt \(y=x^2+4x\) ta được :
\(\left(y-1\right)^2-3y-1=0\)
\(\Leftrightarrow y^2-2y+1-3y-1=0\)
\(\Leftrightarrow y^2-5y=0\)
\(\Leftrightarrow y\left(y-5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=0\\y=5\end{matrix}\right.\)
Với y = 0 ta được \(x^2+4x=0\) \(\Rightarrow x=0\) và \(x=-4\)
Với y = 5 ta được \(x^2+4x=5\) \(\Rightarrow x=1\) và \(x=-5\)
Vậy tổng các giá trị của x là \(0+\left(-4\right)+1+\left(-5\right)=-8\)