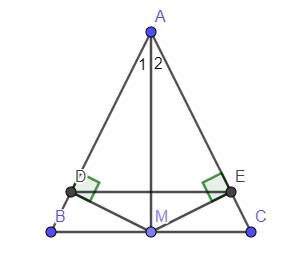
Cho tam giác vuông cân ABC(AB=AC), tia phân giác của góc B&C cắt AC và AB lần lượt tại E và D.
a)Gọi I là giao điểm của BE và CD, cmr \(\Delta MAB;MAC\) là tam giác vuông cân.
b)Từ A và D vẽ các đường thẳng vuông góc với BE, các đường thẳng này cắt BC lần lượt ở K và H.CMR KH=KC.


Hình như đề bị sai hay sao đó bạn
Trên giả thiết không có điểm M, làm sao mà có tam giác MAC; MAB được!
A!Sorry các bạn.AI cắt BC ở M nha!