Trong những hình thoi có chu vi bằng nhau, tìm hình thoi có diện tích lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 2 2017
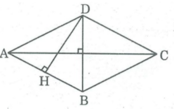
Giả sử có hình thoi ABCD. Kẻ DH ⊥ AB.
Ta có: S A B C D = AB.DH
Tam giác AHD vuông tại H nên: DH ≤ AD
Mà AB = AD (gt)
Nên: S A B C D ≤ A B 2
Vậy S A B C D có giá trị lớn nhất bằng A B 2
Khi đó ABCD là hình vuông.
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.
CM
12 tháng 1 2019
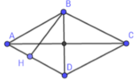
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau. Kẻ BH vuông góc với AD. Ta có SABCD = AD. BH
Trong tam giác vuông ABH vuông tại H thì:
BH ≤ AB (đường vuông góc ngắn hơn đường xiên)
Do đó: SABCD = AD. BH ≤ AD. AB = AB. AB = AB2
SABCDcó giá tị lớn nhất bằng AB2 khi ABCD là hình vuông.
Vây trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.
Đáp án cần chọn là: A
NT
1
31 tháng 3 2018
các hình thoi có cùng chu vi, hình vuông có diện tích lớn nhất.
tk nha bạn
NT
1
8 tháng 12 2017
.Xét hình thoi và hình vuông có cạnh bằng nhau và bằng a. Gọi h là đường cao của hình thoi, ta có : H < và bằng A . Diện tích hình thoi bằng : AH < và bằng A2 , nghĩa là diện tích hình thoi nhỏ hơn hoặc bằng diện tích hình vuông. Vậy trong các hình thoi có cùng chu vi, hình vuông có diện tích lớn nhất.
13 tháng 4 2019
Cạnh của hình thoi là
240 : 4 = 60 (m)
Đường chéo nhỏ dài:
60 : 5/6 = 72 (m)
Đường chéo lớn dài:
60 : 5/8 = 96 (m)
Diện tích khu đất là:
72 x 96 = 6912 (m2)
HH
21 tháng 9 2015
nhầm cách lớp 5 thì làm như thế này
Cạnh hình thoi dài là
576:4=144(cm)
độ dài đường chéo thứ nhất là
3/4 . 144=108(cm)
độ dài đường chéo 2 là
5/6 . 144 =120(cm)
diện tích hình thoi là
(108.120):2=6480(cm2)
21 tháng 9 2015
Chu vi hình thoi gấp 4 lần cạnh hình thoi
Cạnh hình thoi bằng: 576 : 4 = 144 (cm)
Đường chéo thứ nhất bằng: 144 x 3/4 = 108 (cm)
Đường chéo thứ hai bằng: 144 x 5/6 = 120 (cm)
Diện tích hình thoi bằng: (120 x 108) : 2 = 6 480 (cm2)
ĐS:..
21 tháng 4 2023
đây là bài toán hiệu và tỉ.
Ta có: Hiệu số phần bằng nhau là:
7 - 4 = 3(phần)
=> 1 phần ứng với: 9 : 3 = 3 đơn vị
=> đường chéo lớn là: ...
=> đường chéo bé là: ...
Vậy chu vi của HT đó là: ...
diện tích của HT đó là: ...
A A B C D H
Giải
Ta biết diện tích hình thoi ABCD là:
SABCD = AB . DH
Trong tam giác vuông ADH
thì DH \(\le\) AD
nên SABCD = AB . DH \(\le\) AB . AD
Mà AD = AB
nên SABCD \(\le\) AB2
Vậy SABCD có giá trị lớn nhất khi SABCD = AB2 tức là ABCD là hình vuông
Xét hình thoi cạnh a, kẻ đường cao có độ dài h của hình thoi và đặt S là diện tích hình thoi.
Ta có h <= a (quan hệ giữa đường xiên và hình chiếu)
Vì hình thoi cũng là hình bình hành nên :
S =ah
<= a.a = a^2
Vậy max S = a^2
<=> h = a
<=> hình thoi đã cho là hình vuông
Vậy trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.