Giá trị biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BĐT Bunhiacopski:
\(P^2\le3\left(2a+2b+2c\right)=6.2021=12126\)
\(\Leftrightarrow P\le\sqrt{12126}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=\frac{2021}{3}\)

Từ giả thiết:
\(a^2=2\left(b^2+c^2\right)\ge\left(b+c\right)^2\Rightarrow\left(\dfrac{a}{b+c}\right)^2\ge1\Rightarrow\dfrac{a}{b+c}\ge1\)
\(P=\dfrac{a}{b+c}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\ge\dfrac{a}{b+c}+\dfrac{\left(b+c\right)^2}{a\left(b+c\right)+2bc}\ge\dfrac{a}{b+c}+\dfrac{\left(b+c\right)^2}{a\left(b+c\right)+\dfrac{1}{2}\left(b+c\right)^2}\)
\(P\ge\dfrac{a}{b+c}+\dfrac{1}{\dfrac{a}{b+c}+\dfrac{1}{2}}\)
Đặt \(\dfrac{a}{b+c}=x\ge1\)
\(\Rightarrow P\ge x+\dfrac{1}{x+\dfrac{1}{2}}=\dfrac{4}{9}\left(x+\dfrac{1}{2}\right)+\dfrac{1}{x+\dfrac{1}{2}}+\dfrac{5}{9}x-\dfrac{2}{9}\)
\(P\ge2\sqrt{\dfrac{4}{9}\left(x+\dfrac{1}{2}\right).\dfrac{1}{\left(x+\dfrac{1}{2}\right)}}+\dfrac{5}{9}.1-\dfrac{2}{9}=\dfrac{5}{3}\)
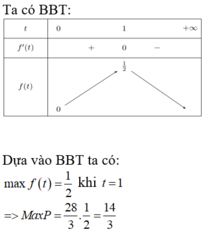
\(P_{min}=\dfrac{5}{3}\) khi \(x=1\) hay \(a=2b=2c\)
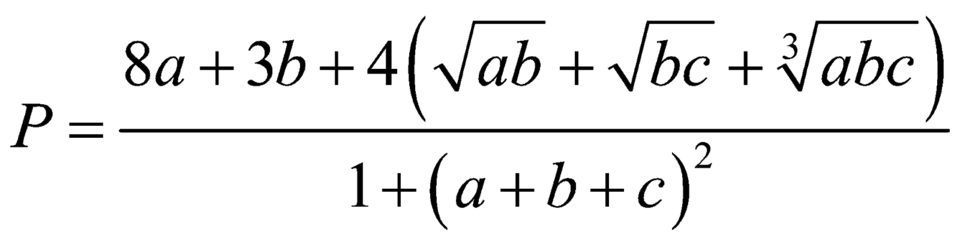
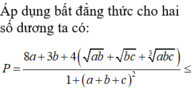
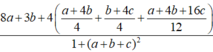
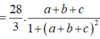
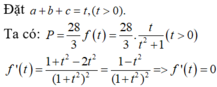
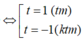
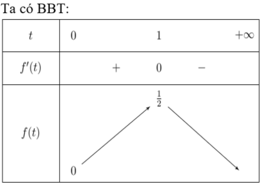

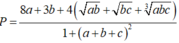 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
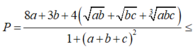
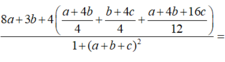
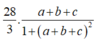
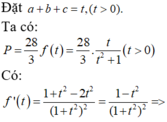
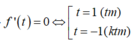
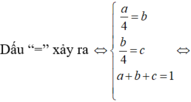
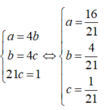
Ta có : \(2x^2+2y^2-2xy+2x+2y+2=0\)
=>\(x^2-2xy+y^2+x^2+2x+1+y^2+2y+1=0\)
=>\(\left(x-y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{\begin{matrix}x-y=0< =>x=y\\x+1=0=>x=-1\\y+1=0=>y=-1\end{matrix}\right.\)
Thế x=-1;y=-1 vào biểu thức , ta có :
\(\left(-1+2\right)^{2016}+\left(-1+1\right)^{2017}=1+0=1\)
\(2x^2+2y^2-2xy+2x+2y+2=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+2x+1\right)+\left(y^2+2y+1\right)=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2=0\)
\(\Leftrightarrow\left[\begin{matrix}\left(x-y\right)^2=0\Leftrightarrow x=y\\\left(x+1\right)^2=0\Leftrightarrow x=-1\\\left(y+1\right)^2=0\Leftrightarrow y=-1\end{matrix}\right.\)
\(A=\left(x+2\right)^{2016}+\left(y+1\right)^{2017}\)
\(A=\left(-1+2\right)^{2016}+\left(-1+1\right)^{2017}\)
\(A=1+0=1\)