Trong mạt phẳng tọa độ vẽ tứ giác ABCD với A(-1;1) , B(2;-2) , C(1;3) , D(3;0) . Hãy chứng tỏ răng A;O;B thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Gọi \(D\left(x;y\right)\) là tọa độ điểm cần tìm.
\(\overrightarrow{AD}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
Tứ giác ABCD là hình bình hành khi và chỉ khi:
\(\overrightarrow{AD}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}x-2=2\\y-4=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)\(\Rightarrow D\left(4;0\right)\).
b) Gọi\(A'\left(x;y\right)\) là điểm cần tìm. A' thỏa mãn hai điều sau:
- \(AA'\perp BC\). (1)
- A' , B, C thẳng hàng. (2)
\(\overrightarrow{AA'}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
\(\left(1\right)\Leftrightarrow\overrightarrow{AA'}.\overrightarrow{BC}=\overrightarrow{0}\)\(\Leftrightarrow2\left(x-2\right)-4\left(y-4\right)=0\) (3)
(2) suy ra hai véc tơ \(\overrightarrow{A'B}\) và \(\overrightarrow{BC}\) cùng phương.
Có \(\overrightarrow{A'B}\left(1-x;3-y\right)\).
Nên \(\dfrac{1-x}{2}=\dfrac{3-y}{4}\) (4)
Từ (3) và (4) suy ra: \(\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\).
Vậy A'(1;3).

Để viết phương trình đường thẳng AB, ta cần tìm được độ dốc và điểm qua của đường thẳng. Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh và tổng các cạnh.
a) Để viết phương trình đường thẳng AB, ta cần tính độ dốc và điểm qua của đường thẳng. Để tính độ dốc, ta sử dụng công thức: m = (y2 - y1) / (x2 - x1), với (x1, y1) và (x2, y2) là hai điểm trên đường thẳng. Ta có A(4, 5) và B(1, -1), áp dụng công thức, ta tính được độ dốc của đường thẳng AB là m = (5 - (-1)) / (4 - 1) = 2.
Để tìm điểm qua của đường thẳng AB, ta có thể sử dụng một trong hai điểm đã cho. Ví dụ, ta sử dụng điểm A(4, 5). Áp dụng công thức: y - y1 = m(x - x1), ta có phương trình đường thẳng AB là y - 5 = 2(x - 4).
Tương tự, để viết phương trình đường thẳng CD, ta tính độ dốc và điểm qua của đường thẳng. Ta có C(4, -4) và D(7, -1), áp dụng công thức, ta tính được độ dốc của đường thẳng CD là m = (-1 - (-4)) / (7 - 4) = 1.
Để tìm điểm qua của đường thẳng CD, ta có thể sử dụng một trong hai điểm đã cho. Ví dụ, ta sử dụng điểm C(4, -4). Áp dụng công thức: y - y1 = m(x - x1), ta có phương trình đường thẳng CD là y - (-4) = 1(x - 4).
b) Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh và tổng các cạnh. Ta có A(4, 5), B(1, -1), C(4, -4), D(7, -1). Để tính độ dài cạnh AB, ta sử dụng công thức khoảng cách giữa hai điểm: AB = √((x2 - x1)^2 + (y2 - y1)^2). Áp dụng công thức, ta tính được AB = √((1 - 4)^2 + (-1 - 5)^2) = √((-3)^2 + (-6)^2) = √(9 + 36) = √45.
Tương tự, ta tính được CD = √((7 - 4)^2 + (-1 - (-4))^2) = √(3^2 + 3^2) = √(9 + 9) = √18.
Để tính chu vi tứ giác ABCD, ta cộng tổng độ dài các cạnh: chu vi = AB + BC + CD + DA = √45 + BC + √18 + DA.
Tuy nhiên, để tính độ dài cạnh BC và DA, cần có thêm thông tin về các điểm trên đường thẳng BC và DA. Vì vậy, để tính chu vi tứ giác ABCD, cần có thêm thông tin.

a) Để viết phương trình đường thẳng AB, CD, DA, ta có thể sử dụng công thức phương trình đường thẳng đi qua hai điểm.
Phương trình đường thẳng AB: Điểm A(4,5) và B(1,-1) Ta có: Độ dốc của đường thẳng AB: m = (y2 - y1) / (x2 - x1) = (-1 - 5) / (1 - 4) = -2 Phương trình đường thẳng AB: y - y1 = m(x - x1) => y - 5 = -2(x - 4) => y - 5 = -2x + 8 => 2x + y = 13
Phương trình đường thẳng CD: Điểm C(4,-4) và D(7,-1) Ta có: Độ dốc của đường thẳng CD: m = (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (7 - 4) = 1 Phương trình đường thẳng CD: y - y1 = m(x - x1) => y - (-1) = 1(x - 7) => y + 1 = x - 7 => x - y = 8
Phương trình đường thẳng DA: Điểm D(7,-1) và A(4,5) Ta có: Độ dốc của đường thẳng DA: m = (y2 - y1) / (x2 - x1) = (5 - (-1)) / (4 - 7) = -2 Phương trình đường thẳng DA: y - y1 = m(x - x1) => y - (-1) = -2(x - 7) => y + 1 = -2x + 14 => 2x + y = 13
b) Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh của tứ giác.
Độ dài cạnh AB: AB = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(1 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Độ dài cạnh BC: BC = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(4 - 1)^2 + (-4 - (-1))^2] = √[9 + 9] = √18
Độ dài cạnh CD: CD = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - (-4))^2] = √[9 + 9] = √18
Độ dài cạnh DA: DA = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Từ đó, chu vi tứ giác ABCD là: AB + BC + CD + DA = √45 + √18 + √18 + √45.
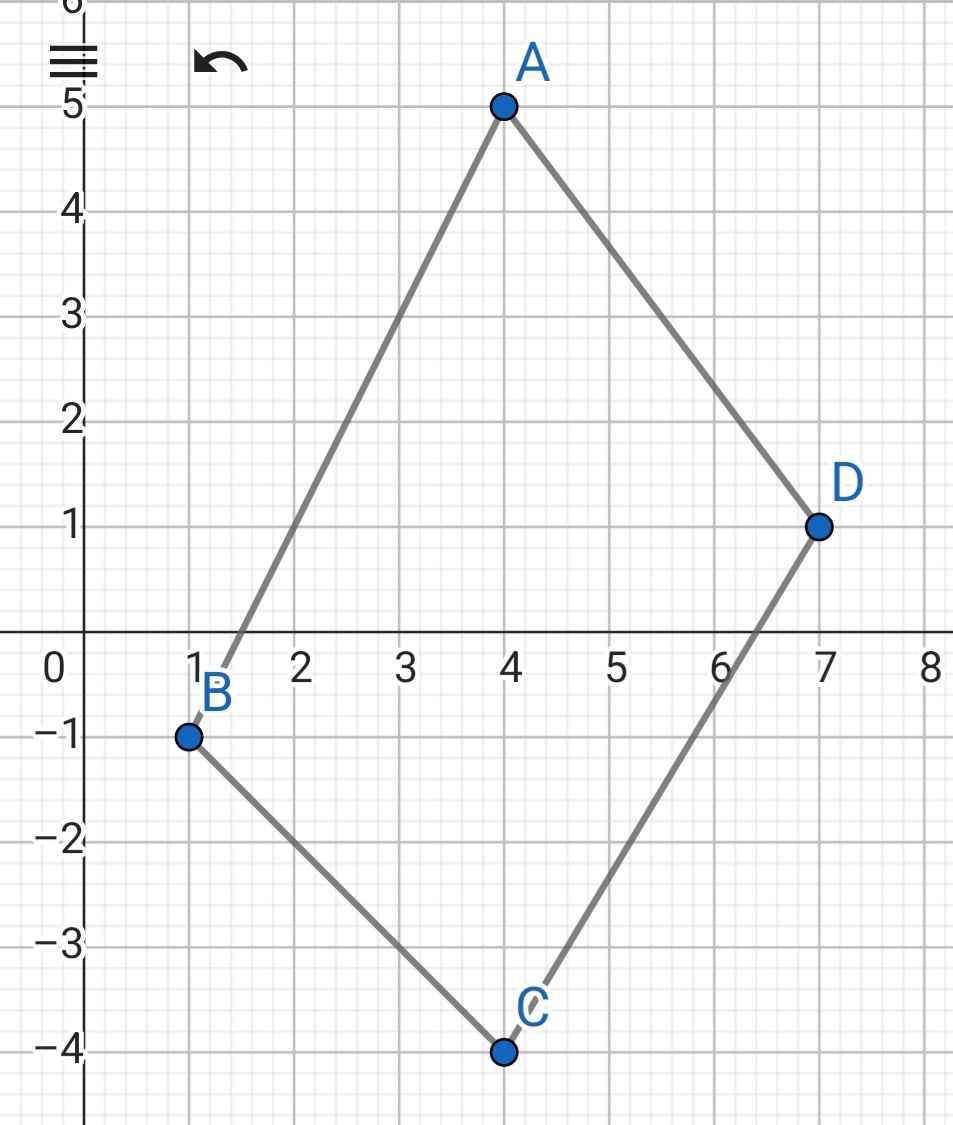 a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
Do (d) đi qua A nên:
4a + b = 5
⇔ b = 5 - 4a (1)
Do (d) đi qua B nên:
a + b = -1 (2)
Thay (1) vào (2) ta được:
a + 5 - 4a = -1
⇔ -3a = -6
⇔ a = 2
Thay a = 2 vào (1) ta được:
b = 5 - 4.2 = -3
Vậy (d): y = 2x - 3
* Gọi (d'): y = ax + b là phương trình đường thẳng CD
Do (d') đi qua C nên:
4a + b = -4
⇔ b = -4 - 4a (3)
Do (d') đi qua D nên:
7a + b = -1 (4)
Thay (3) vào (4) ta được:
7a - 4 - 4a = -1
⇔ 3a = 3
⇔ a = 1
Thay a = 1 vào (3) ta được:
b = -4 - 4.1 = -8
Vậy (d'): y = x - 8
* Gọi (d''): y = ax + b là phương trình đường thẳng DA
Do (d'') di qua D nên:
7a + b = -1
⇔ b = -1 - 7a (5)
Do (d'') đi qua A nên:
4a + b = 5 (6)
Thay (5) vào (6) ta được:
4a - 1 - 7a = 5
⇔ -3a = 6
⇔ a = -2
Thay a = -2 vào (5) ta được:
b = -1 - 7.(-2) = 13
Vậy (d''): y = -2x + 13
b) Ta có:
AB² = 3² + 6² = 45
⇒ AB = 3√5
BC² = 3² + 3² = 18
⇒ BC = 3√2
CD² = 3² + 5² = 34
⇒ CD = √34
AD² = 3² + 4² = 25
⇒ AD = 5
Chu vi tứ giác ABCD:
3√5 + 3√2 + √34 + 5

a: Tọa độ trọng tâm là:
\(\left\{{}\begin{matrix}x=\dfrac{1+3+5}{3}=3\\y=\dfrac{1+5-1}{3}=\dfrac{5}{3}\end{matrix}\right.\)
b: \(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AD}=\left(x-1;y-1\right)\)
Để BC//AD và BC=2AD thì 2=2(x-1) và -6=2(y-1)
=>x-1=1 và y-1=-3
=>x=2 và y=-2

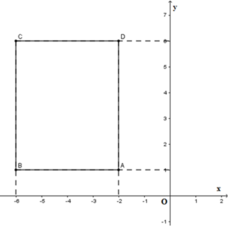
Vẽ các điểm A(-2;1);B(-6;1);C(-6;6) và D(-2;6) trên cùng mặt phẳng tọa độ
Ta thấy ABCD là hình chữ nhật
Đáp án cần chọn là B

Hình chữ nhật ABDC có AB=5cm;AC=3cm nên diện tích ABDCABDC bằng 5.3=15( cm 2 )
Đáp án cần chọn là: A

Vẽ các điểm A(3;1);B(-2;1);C(3;4) và D(-2;4) trên cùng mặt phẳng tọa độ
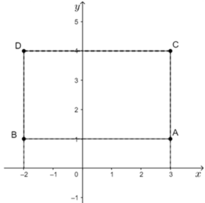
Theo hình vẽ ta thấy ABCD là hình chữ nhật
Đáp án cần chọn là B





\(\overrightarrow{AO}=\left(1;-1\right)\)
\(\overrightarrow{AB}=\left(3;-3\right)\)
Vì \(\dfrac{1}{3}=\dfrac{-1}{-3}\)
nên A,O,B thẳng hàng