x^2-11x+28
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 8 2021
\(\left(x^2-3x\right)\left(x^2-11x+28\right)=x^4-11x^3+28x^2-3x^3+33x^2-84x=x^4-14x^3+61x^2-84x\)
TB
2
29 tháng 10 2022
Do
Dấu “=” xảy ra khi
Vậy giá trị nhỏ nhất của khi và
DT
0
LB
1
HV
8 tháng 1 2018
(x2-11x+28)(x2-7x+10)-72=0
(x-2)(x-7)(x-4)(x-5)-72=0
(x2-9x+14)(x2-9x+20)-72=0
Đặt x2-9x+14=a, ta có
a(a+6)-72=0
a2+6a-72=0
a2+6a+9-81=0
(a+3)2=81
=> a+3=9 => a=6=> x2-9x+14=6
=>x2-9x+8=0
=> (x-1)(x-8)=0
=> x=1 hoặc x=8
Vậy............ !!!!!
NN
4
KT
13 tháng 2 2020
\(x^2+11x+28\)
\(=\left(x^2+4x\right)+\left(7x+28\right)\)
\(=x\left(x+4\right)+7\left(x+4\right)\)
\(=\left(x+4\right)\left(x+7\right)\)
16 tháng 4 2016
Giải Phương Trình Sau (Nhớ ghi cách làm nha mình k đúng cho)
KH
1
28 tháng 3 2021
\(\left\{{}\begin{matrix}x^2+y^4+xy=2xy^2+7\\xy^3-x^2y+4xy+11x=28+11y^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-y^2\right)^2+xy-7=0\\\left(x^{ }-y^2\right)\left(11-xy\right)+4\left(xy-7\right)=0\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x-y^2=a\\xy-7=b\end{matrix}\right.\) hệ trở thành \(\left\{{}\begin{matrix}a^2+b=0\\a\left(4-b\right)+4b=0\end{matrix}\right.\)\(\Rightarrow a\left(4+a^2\right)-4a^2=0\Leftrightarrow a\left(a^2-4a+4\right)=0\Leftrightarrow a\left(a-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}a=0;b=0\\a=2;b=-4\end{matrix}\right.\)
Giải từng trường hợp rồi kết hợp nghiệm
G
0
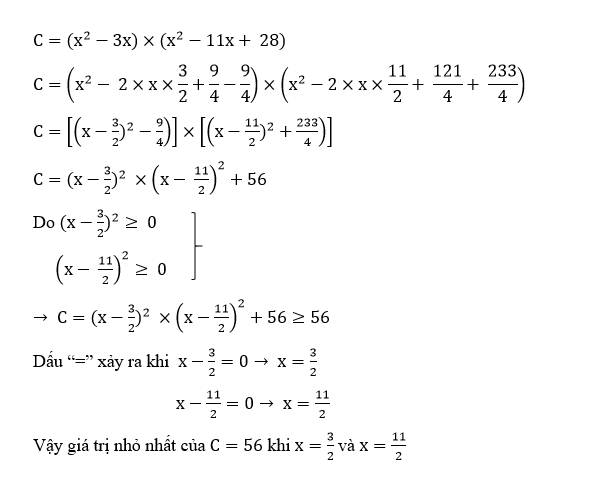
\(x^2-11x+28\)
\(=x^2-4x-7x+28=x\left(x-4\right)-7\left(x-4\right)=\left(x-7\right)\left(x-4\right)\)