Giúp vs mọi người ơi !!! Bài bài cũng đc ah.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


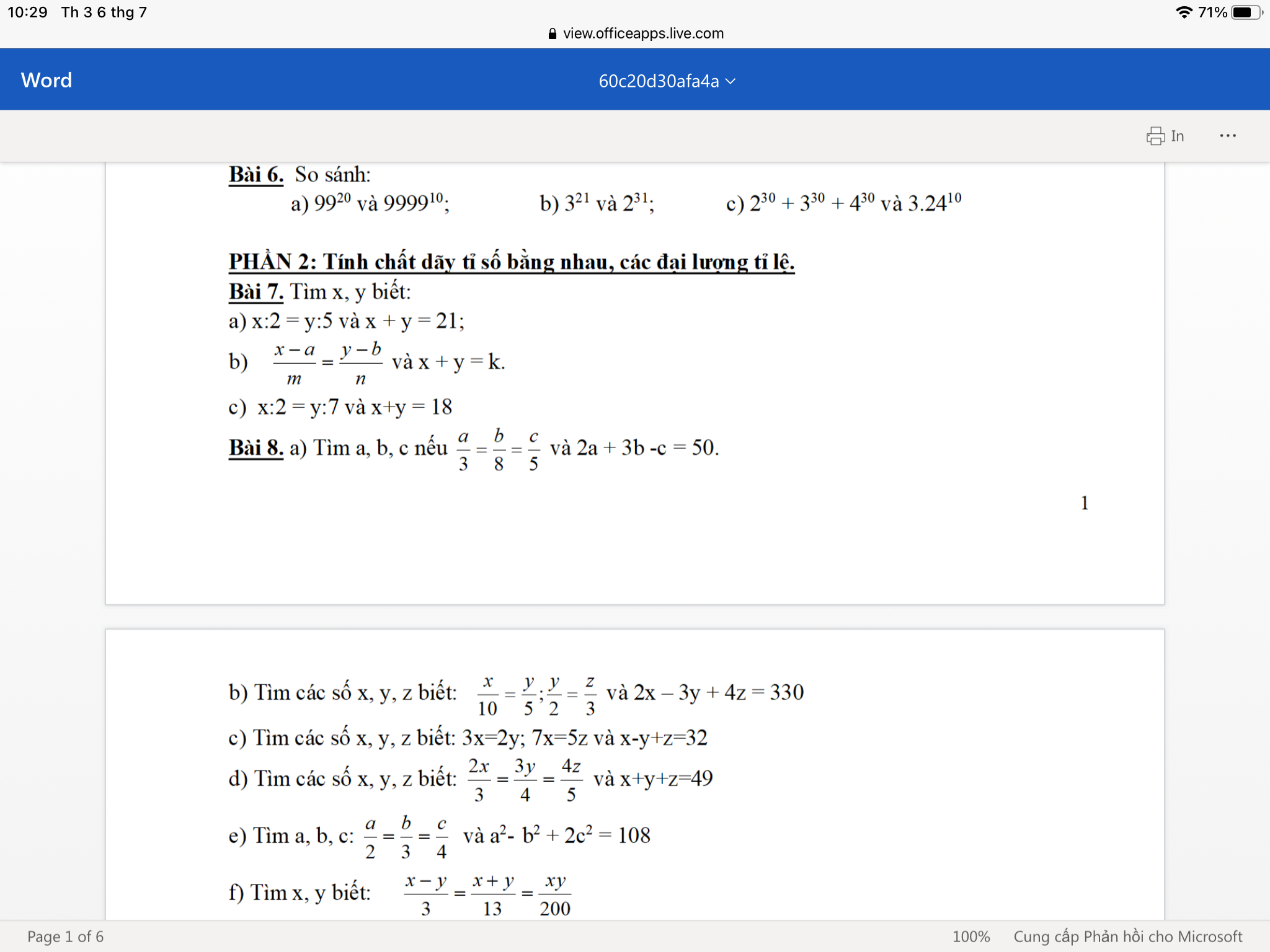
Bài 7:
a) Ta có: x:2=y:5
nên \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=3\\\dfrac{y}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=15\end{matrix}\right.\)
c) Ta có: x:2=y:7
nên \(\dfrac{x}{2}=\dfrac{y}{7}\)
mà x+y=18
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{7}=\dfrac{x+y}{2+7}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=2\\\dfrac{y}{7}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=14\end{matrix}\right.\)
Bài 8:
a) Ta có: \(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\)
nên \(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}\)
mà 2a+3b-c=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}=\dfrac{2a+3b-c}{6+24-5}=\dfrac{50}{25}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{3}=2\\\dfrac{b}{8}=2\\\dfrac{c}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=16\\c=10\end{matrix}\right.\)
Bài 8:
b) Ta có: \(\dfrac{x}{10}=\dfrac{y}{5}\)
nên \(\dfrac{x}{20}=\dfrac{y}{10}\)(1)
Ta có: \(\dfrac{y}{2}=\dfrac{z}{3}\)
nên \(\dfrac{y}{10}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
\(\Leftrightarrow\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}\)
mà 2x-3y+4z=330
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}=\dfrac{2x-3y+4z}{40-30+60}=\dfrac{330}{70}=\dfrac{33}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{20}=\dfrac{33}{7}\\\dfrac{y}{10}=\dfrac{33}{7}\\\dfrac{z}{15}=\dfrac{33}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{660}{7}\\y=\dfrac{330}{7}\\z=\dfrac{495}{7}\end{matrix}\right.\)
c) Ta có: 3x=2y
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
hay \(\dfrac{x}{10}=\dfrac{y}{15}\)(1)
Ta có: 7x=5z
nên \(\dfrac{x}{5}=\dfrac{z}{7}\)
hay \(\dfrac{x}{10}=\dfrac{z}{14}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}\)
mà x-y+z=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}=\dfrac{x-y+z}{10-15+14}=\dfrac{32}{9}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{10}=\dfrac{32}{9}\\\dfrac{y}{15}=\dfrac{32}{9}\\\dfrac{z}{14}=\dfrac{32}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{320}{9}\\y=\dfrac{480}{9}=\dfrac{160}{3}\\z=\dfrac{448}{9}\end{matrix}\right.\)



4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19

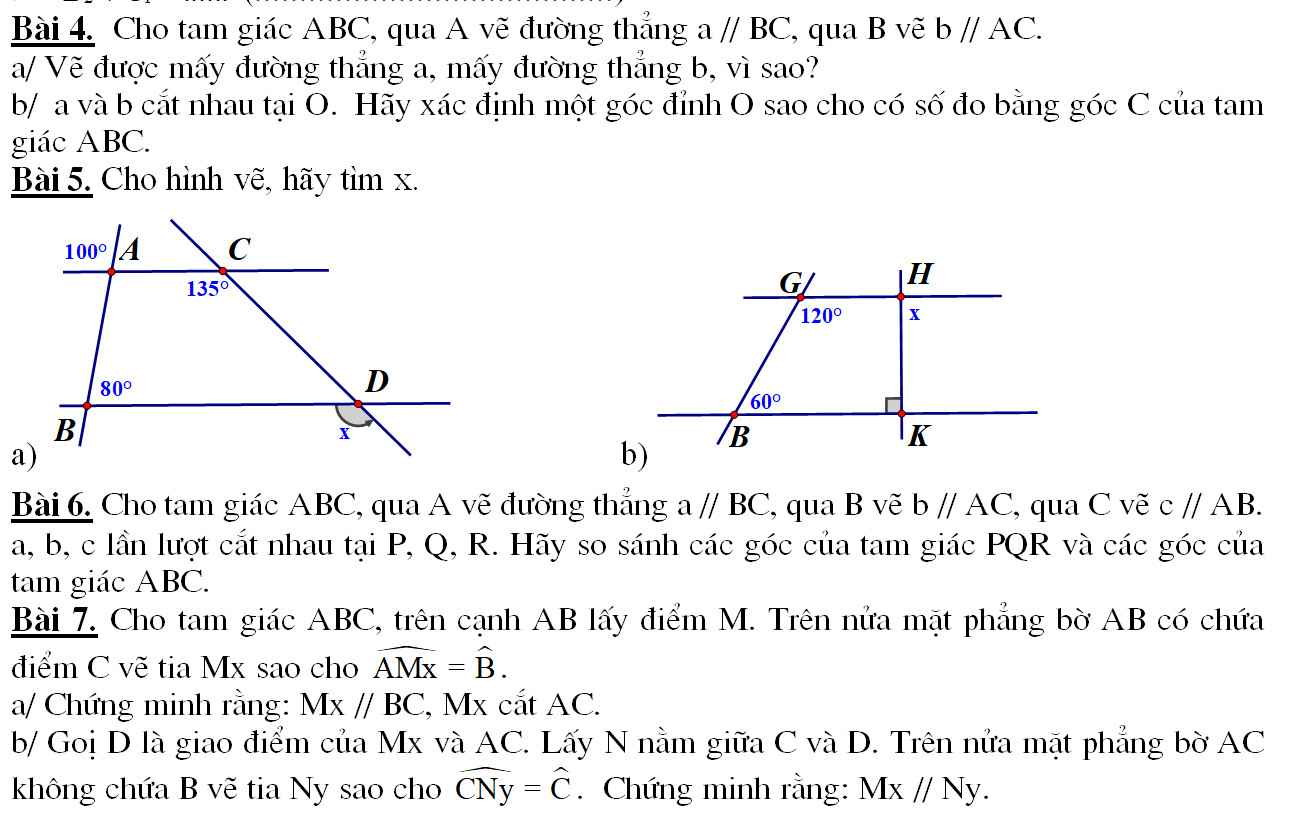
Bài 5:
A 1 2 3 4 B 1 C 1 D 1
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
G H B K 1 1 1 1
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)

11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)


1 correct
2 incorrect
3 incorrect
4 correct
5 incorrect
6 correct
7 correct
8 incorrect
9 incorrect
10 correct












Bài 4 :
\(M=\left(2x-3y\right)^2-\left(3y-2\right)\left(3y+2\right)-\left(1-2x\right)^2+4x\left(3y-1\right)\)
\(=\left(2x-3y-1+2x\right)\left(2x-3y+1-2x\right)-9y^2+4+12xy-4x\)
\(=\left(4x-3y-1\right)\left(1-3y\right)-9y^2+4+12xy-4x\)
\(=4x-12xy-3y+9y^2-1+3y-9y^2+4+12xy-4x=3\)
Vậy biểu thức ko phụ thuộc giá trị biến x
Bài 2 :
a, \(\left(a-3b\right)^2=a^2-6ab+9b^2\)
b, \(x^2-16y^4=\left(x-4y^2\right)\left(x+4y^2\right)\)
c, \(25a^2-\frac{1}{4}b^2=\left(5a-\frac{1}{2}b\right)\left(5a+\frac{1}{2}b\right)\)
Bài 3 :
a, \(9x^2-6x+1=\left(3x-1\right)^2\)
b, \(\left(2x+3y\right)^2+2\left(2x+3y\right)+1=\left(2x+3y+1\right)^2\)
c, \(4\left(2x-y\right)^2-8x+4y+1=\left(4x-2y\right)^2-2\left(4x-2y\right)+1=\left(4x-2y-1\right)^2\)