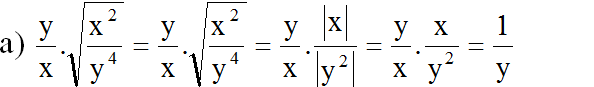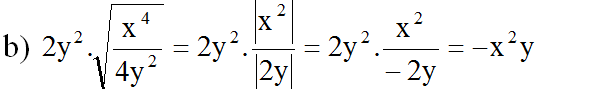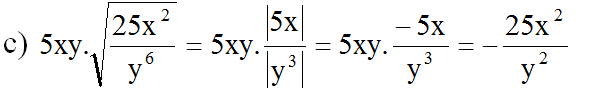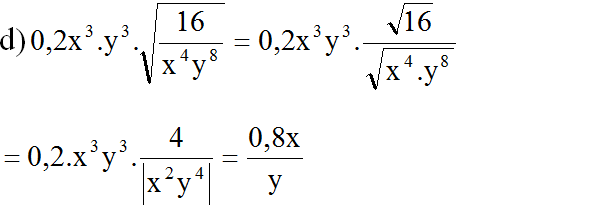So sánh: \(\dfrac{x-y}{x+y}\) và \(\dfrac{x^2-y^2}{x^2+xy+y^2}\) với x>y>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
10 tháng 8 2021
Đúng(3)
Những câu hỏi liên quan
13 tháng 2 2018
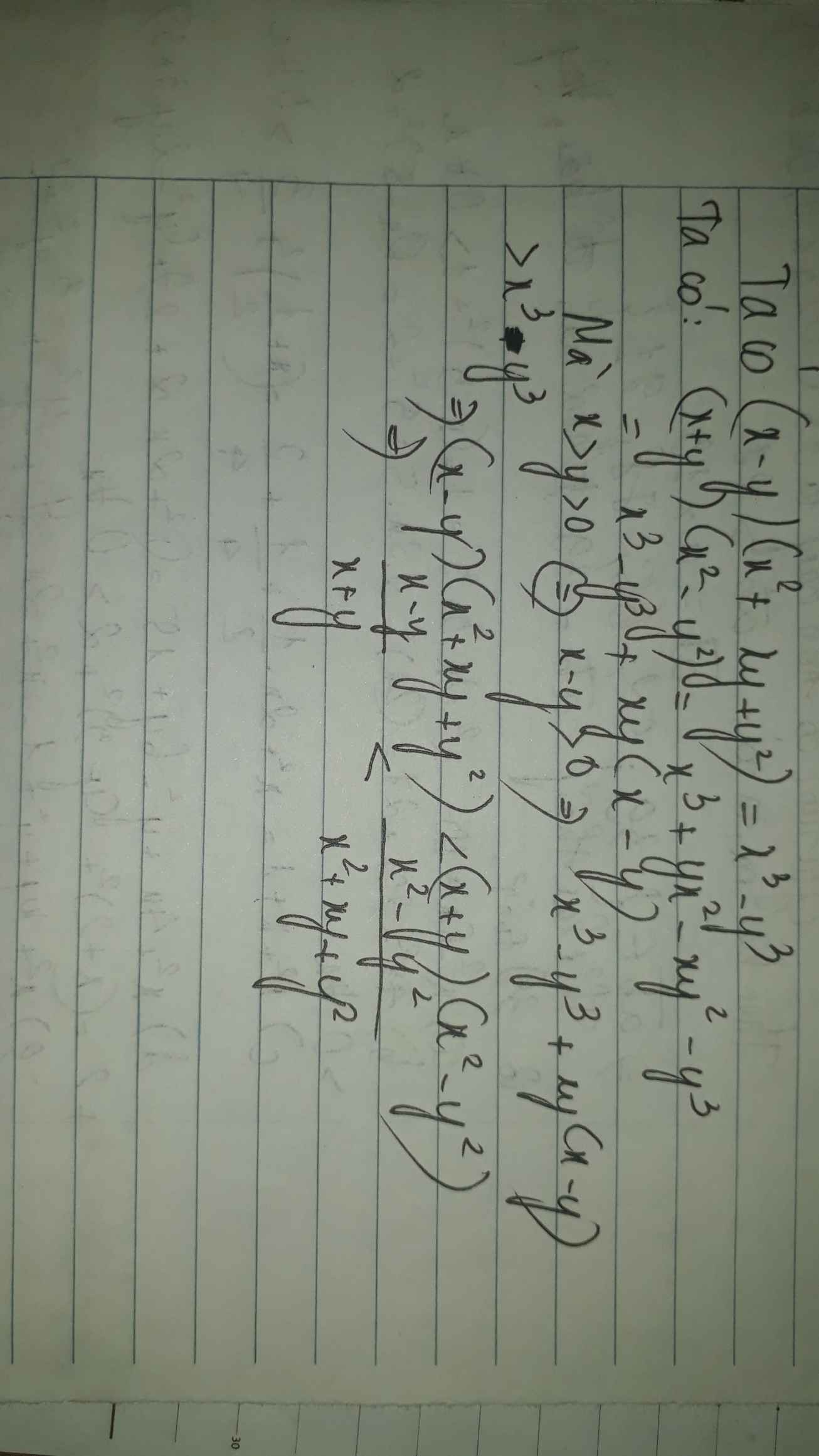
theo đầu bài ta có\(\dfrac{x^2+y^2}{xy}=\dfrac{10}{3}\)=>\(3x^2+3y^2=10xy\)
A=\(\dfrac{x-y}{x+y}\)
=>\(A^2=\left(\dfrac{x-y}{x+y}\right)^2=\dfrac{x^2-2xy+y^2}{x^2+2xy+y^2}=\dfrac{3x^2-6xy+3y^2}{3x^2+6xy+3y^2}=\dfrac{10xy-6xy}{10xy+6xy}=\dfrac{4xy}{16xy}=\dfrac{1}{4}\)
=>A=\(\sqrt{\dfrac{1}{4}}=\dfrac{-1}{2}hoặc\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\) (cộng trừ căn 1/4 nhé)
vì y>x>0=> A=-1/2
24 tháng 9 2022
a: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{3}=\dfrac{13}{6}\sqrt{6}-2\sqrt{3}\)
b: \(VT=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\cdot\left(\sqrt{x}+\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)^2\)
c: \(VT=\dfrac{\sqrt{y}}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{\sqrt{x}}{\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)}\)
\(=\dfrac{y-x}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{-\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)
17 tháng 5 2017
Với x,y,z dương
Ta có:(x-y)2\(\ge0\forall x;y\)
=>x2+y2\(\ge\)2xy
Dấu = xảy ra khi x=y
Tương tự y2+z2\(\ge\)2yz
z2+x2\(\ge\)2zx
Cộng vế với vế 3 BĐT =>2(x2+y2+z2)\(\ge\)2(xy+yz+zx)
<=>x2+y2+z2\(\ge\)xy+yz+zx
<=>\(\dfrac{3}{xy+yz+zx}\ge\dfrac{3}{x^2+y^2+z^2}\)
Dấu = xảy ra khi và chỉ khi x=y=z
=>\(\dfrac{3}{xy+yz+zx}+\dfrac{2}{x^2+y^2+z^2}\ge\dfrac{5}{x^2+y^2+z^2}\)
Áp dụng BĐT bunhiacopski:
\(\left(x^2+y^2+z^2\right)\left(\dfrac{1}{3^2}+\dfrac{1}{3^2}+\dfrac{1}{3^3}\right)\le\left(\dfrac{x+y+z}{3}\right)^2=\dfrac{1}{3^2}=\dfrac{1}{9}\)(Do x+y+z=1)
Dấu = xảy ra khi và chỉ khi \(\dfrac{x}{3}=\dfrac{y}{3}=\dfrac{z}{3}\)<=>x=y=z
=>\(\dfrac{5}{x^2+y^2+z^2}=\dfrac{5}{3\cdot\left(x^2+y^2+z^2\right)\left(\dfrac{1}{3^2}+\dfrac{1}{3^2}+\dfrac{1}{3^2}\right)}\ge\dfrac{5}{3\cdot\dfrac{1}{9}}=15\)
=>\(\dfrac{3}{xy+yz+zx}+\dfrac{2}{x^2+y^2+z^2}\ge15\)(đpcm)
Dấu = xảy ra khi \(\left\{{}\begin{matrix}x=y=z\\z+y+z=1\end{matrix}\right.\)<=>x=y=z=\(\dfrac{1}{3}\)
13 tháng 5 2018
Với \(x=y=2\) thì \(Q=\dfrac{10}{3}\)
Ta sẽ chứng minh \(\dfrac{10}{3}\) là GTNN của \(Q\)
Thật vậy: \(\dfrac{\left(x+y+2\right)^2}{xy+2\left(x+y\right)}+\dfrac{xy+2\left(x+y\right)}{\left(x+y+2\right)^2}\ge\dfrac{10}{3}\)
\(\Leftrightarrow\dfrac{\left(x^2-xy-2x+y^2-2y+4\right)\left(3x^2+5xy+10x+3y^2+10y+12\right)}{3\left(x+y+2\right)^2\left(xy+2x+2y\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(\left(2x-y-2\right)^2+3\left(y-2\right)^2\right)\left(3x^2+5xy+10x+3y^2+10y+12\right)}{12\left(x+y+2\right)^2\left(xy+2x+2y\right)}\ge0\)
BĐT cuối đúng với \(x;y>0\)
Vậy \(Q_{Min}=\dfrac{10}{3}\Leftrightarrow x=y=2\)
18 tháng 5 2018
Quỳnh Hoa Lenka: Cách của mình đúng và được chấp nhận khi thi nhé :) cho nên mình cũng ko đòi hòi 1 lời giải nào hơn
T
19 tháng 4 2021
(Vì x > 0 nên |x| = x; y2 > 0 với mọi y ≠ 0)
(Vì x2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên |y3| = y3)
(Vì x2y4 = (xy2)2 > 0 với mọi x ≠ 0, y ≠ 0)
7 tháng 10 2022
a: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{6}\)
\(=\dfrac{1}{6}\sqrt{6}\)
b: \(VT=\dfrac{\sqrt{y}}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{\sqrt{x}}{\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)}\)
\(=\dfrac{y-x}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{-\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)
4 tháng 9 2022
\(A=\left(\dfrac{4\sqrt{xy}+x-2\sqrt{xy}+y}{2\left(x-y\right)}\right)\cdot\dfrac{2\sqrt{x}}{\sqrt{x}+\sqrt{y}}-\dfrac{\sqrt{y}}{\sqrt{x}-\sqrt{y}}\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{\left(x-y\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}}-\dfrac{\sqrt{y}}{\sqrt{x}-\sqrt{y}}\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{x}-\sqrt{y}}=1\)
28 tháng 2 2018
Áp dụng BĐT Cô si cho 2 số dương a,b ta có \(\dfrac{a+b}{2}\ge\sqrt{ab}\)
\(\dfrac{1}{a}+\dfrac{1}{b}\ge2.\sqrt{\dfrac{1}{a}.\dfrac{1}{b}}=>\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge2\sqrt{ab}.2\sqrt{\dfrac{1}{a}.\dfrac{1}{b}}\)
suy ra \(\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge4\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\).Áp dụng vào bài toán ta có :\(\dfrac{1}{x^2+xy}+\dfrac{1}{y^2+xy}\ge\dfrac{4}{x^2+xy+y^2+xy}=\dfrac{4}{\left(x+y\right)^2}\ge4\) (Do \(x+y\le1\))