cho dãy số (sn) với sn=sin(4n−1)\(\frac{\pi}{6}\) .
chứng minh rằng sn=sn+3 với mọi n≥1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
0
17 tháng 8 2023
a: S8={1;2;4;8}
S9={1;3;9}
S12={1;2;3;4;6;12}
b: M chia hết cho n
=>\(n\inƯ\left(m\right)\)
=>Ước của n chắc chắn sẽ là ước của m
=>\(S_n\subset S_M\)
c: \(S_n\subset S_m\)
=>Ước của n là ước của m
=>n là ước của m
=>\(m⋮n\)
CM
19 tháng 12 2019
iểm tra với n = 1
Giả sử đã có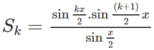 
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
CM
24 tháng 6 2018
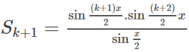
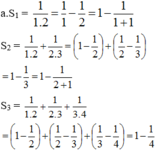
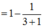
b. Dự đoán: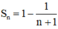 
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
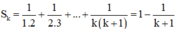
Khi đó:
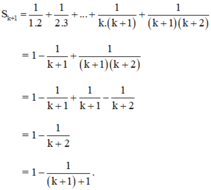
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
