-3x^2-9x+12=3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
12 tháng 2 2018
a) \(2\left(9x^2+6x+1\right)=\left(3x+1\right)\left(x-2\right)\)
\(\Leftrightarrow\)\(2\left(3x+1\right)^2-\left(3x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\)\(\left(3x+1\right)\left[2\left(3x+1\right)-\left(x-2\right)\right]=0\)
\(\Leftrightarrow\)\(\left(3x+1\right)\left(6x+2-x+2\right)=0\)
\(\Leftrightarrow\)\(\left(3x+1\right)\left(5x+4\right)=0\)
đến đây tự lm nha
b) \(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\) (1)
ĐKXĐ: \(x\ne\pm\frac{1}{3}\)
\(\left(1\right)\)\(\Leftrightarrow\)\(\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)
\(\Rightarrow\)\(\left(1-3x\right)^2-\left(1+3x\right)^2=12\)
\(\Leftrightarrow\)\(\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)
\(\Leftrightarrow\)\(-12x=12\)
\(\Leftrightarrow\)\(x=-1\) (t/m ĐKXĐ)
Vậy....
12 tháng 2 2018
a) \(2\left(9x^2+6x+1\right)=\left(3x+1\right)\left(x-2\right)\)
\(\Leftrightarrow2\left(3x+1\right)^2-\left(3x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left[2\left(3x+1\right)-\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(3x+1\right)\left(6x+2-x+2\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\5x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=-\frac{4}{5}\end{cases}}}\)
b) ĐKXĐ: \(x\ne\pm\frac{1}{3}\)
\(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)
\(\Leftrightarrow\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)
\(\Leftrightarrow\left(1-3x\right)^2-\left(1+3x\right)^2=12\)
\(\Leftrightarrow\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)
\(\Leftrightarrow-12x=12\)
\(\Leftrightarrow x=-1\) (thỏa mãn)
Vậy x = -1
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
VN
16 tháng 1 2017
a)
<=> 3x - 3 + x - 2 = 2x - 2 - x + 1
<=> 3x + x - 2x + x = -2 + 1 + 3 + 2
<=> 3x = 4
<=> x = 4/3
Các câu sau làm tương tự
29 tháng 9 2018
\(\left(3x-3\right)+\left(x-2\right)=\left(2x-2\right)-\left(x-1\right)\)
<=> \(3x-3+x-2=2x-2-x+1\)
<=> \(4x-5=x-1\)
<=> \(3x=4\)
<=> \(x=\frac{4}{3}\)
Vậy....
11 tháng 4 2020
a/2(9x2+6x+1)=(3x+1)(x-2)
⇔2(3x+1)2= (3x+1)(x-2)
⇔ 2(3x+1)2 :(3x+1)=x-2
⇔ 2(3x+1)=x-2
⇔6x+2-x+2=0
⇔5x+4=0
⇔5x=-4
⇔x=\(\frac{-4}{5}\)
b/\(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)
⇔\(\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)
⇔12=(1-3x)2-(1+3x)2
⇔-(1-3x-1-3x)(1-3x+1+3x)=--12
⇔-(-6x.2)=-12
⇔12x=-12
⇔x=-1
bạn thấy mình làm sai hay thiếu thì bạn nhớ nhắc mình nha.
MH
4 tháng 10 2021
c) \(\sqrt{\left(x-2\right)^2}=10\)
\(x-2=10\)
\(x=12\)
d) \(\sqrt{9x^2-6x+1}=15\)
\(\sqrt{\left(3x\right)^2-2.3x.1+1^2}=15\)
\(\sqrt{\left(3x-1\right)^2}=15\)
\(3x-1=15\)
\(3x=16\)
\(x=\dfrac{16}{3}\)
4 tháng 10 2021
a) \(đk:x\ge0\)
\(pt\Leftrightarrow3\sqrt{2x}+4\sqrt{2x}-3\sqrt{2x}=12\)
\(\Leftrightarrow4\sqrt{2x}=12\Leftrightarrow\sqrt{2x}=3\Leftrightarrow2x=9\Leftrightarrow x=\dfrac{9}{2}\left(tm\right)\)
b) \(đk:x\ge-2\)
\(pt\Leftrightarrow3\sqrt{x+2}+12\sqrt{x+2}-2\sqrt{x+2}=26\)
\(\Leftrightarrow13\sqrt{x+2}=26\)
\(\Leftrightarrow\sqrt{x+2}=2\Leftrightarrow x+2=4\Leftrightarrow x=2\left(tm\right)\)
c) \(pt\Leftrightarrow\left|x-2\right|=10\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=10\\x-2=-10\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-8\end{matrix}\right.\)
d) \(pt\Leftrightarrow\sqrt{\left(3x-1\right)^2}=15\)
\(\Leftrightarrow\left|3x-1\right|=15\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=15\\3x-1=-15\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{16}{3}\\x=-\dfrac{14}{3}\end{matrix}\right.\)
e) \(đk:x\ge\dfrac{8}{3}\)
\(pt\Leftrightarrow3x+4=9x^2-48x+64\)
\(\Leftrightarrow9x^2-51x+60=0\)
\(\Leftrightarrow3\left(x-4\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)
22 tháng 3 2021
a) Ta có: \(\dfrac{x+5}{3x-6}-\dfrac{1}{2}=\dfrac{2x-3}{2x-4}\)
\(\Leftrightarrow\dfrac{2\left(x+5\right)}{6\left(x-2\right)}-\dfrac{3\left(x-2\right)}{6\left(x-2\right)}=\dfrac{3\left(2x-3\right)}{6\left(x-2\right)}\)
Suy ra: \(2x+5-3x+6=6x-9\)
\(\Leftrightarrow-x+11-6x+9=0\)
\(\Leftrightarrow20-7x=0\)
\(\Leftrightarrow7x=20\)
hay \(x=\dfrac{20}{7}\)(thỏa ĐK)
Vậy: \(S=\left\{\dfrac{20}{7}\right\}\)
FY
0
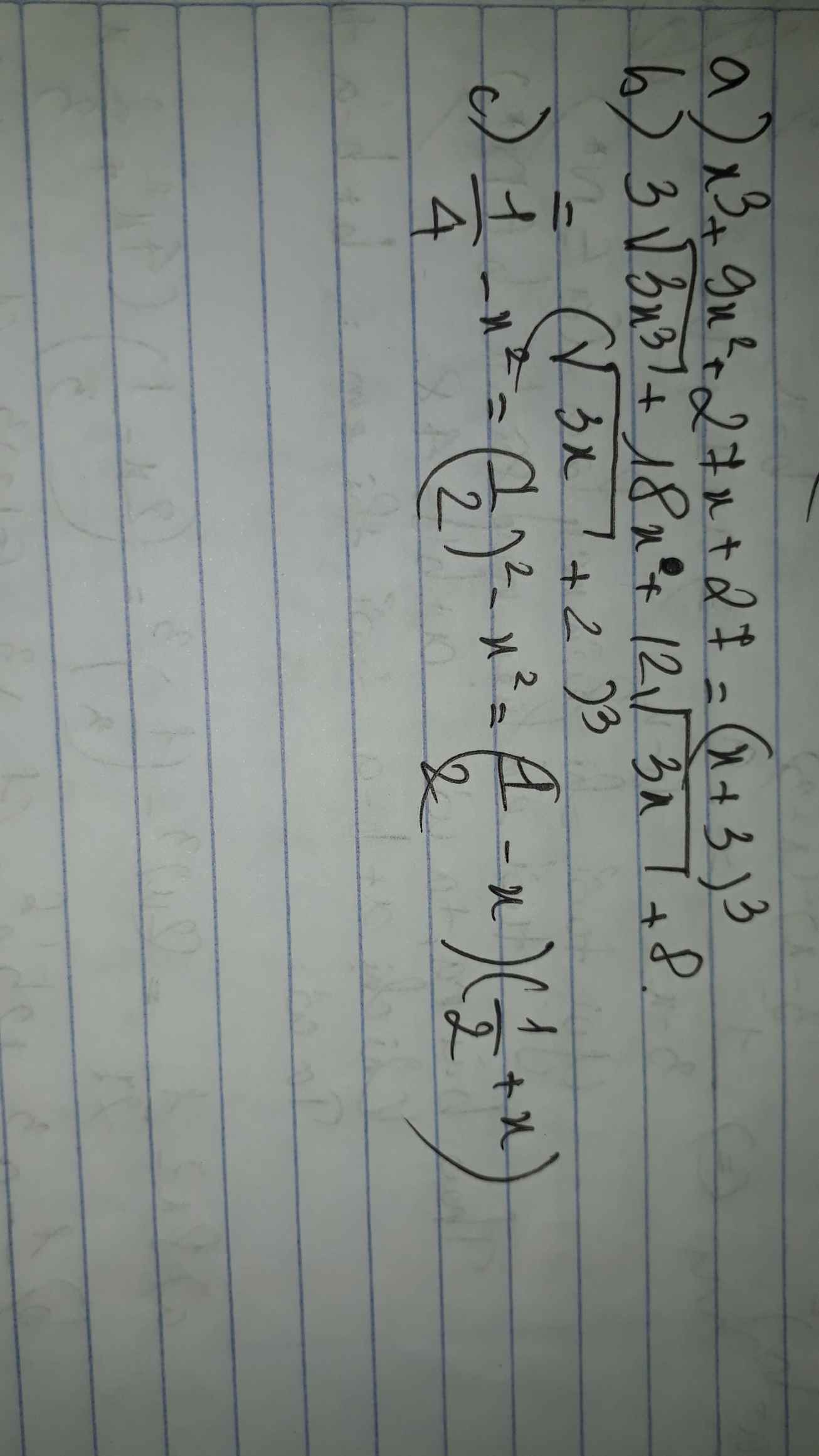
\(-3x^2-9x+12=3\Leftrightarrow-3x^2-9x+9=0\)
\(\Leftrightarrow-3\left(x^2+3x-3\right)=0\)
\(\Leftrightarrow x^2+3x-3=0\Leftrightarrow x^2+2.\frac{3}{2}x+\frac{9}{4}-\frac{9}{4}-3=0\)
\(\Leftrightarrow\left(x+\frac{3}{2}\right)^2-\frac{21}{4}=0\Leftrightarrow\left(x+\frac{3}{2}\right)^2-\left(\frac{\sqrt{21}}{2}\right)^2=0\)
\(\Leftrightarrow\left(x+\frac{3}{2}-\frac{\sqrt{21}}{2}\right)\left(x+\frac{3}{2}+\frac{\sqrt{21}}{2}\right)=0\)
\(\Leftrightarrow\left(x+\frac{3-\sqrt{21}}{2}\right)\left(x+\frac{3+\sqrt{21}}{2}\right)=0\Leftrightarrow x=-\frac{3\pm\sqrt{21}}{2}\)