Cho tứ giác MNPQ có 2 đường chéo cắt nhau tại E và có cạnh MN=MQ;NP=PQ.Chứng minh a)MP là đường phân giác của góc M và P b) MP vuông góc với NQ Mn giúp em với Em cảm ơn ạ❤️
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và \(QP=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MN//QP và MN=QP
Xét tứ giác MNPQ có
MN//QP(cmt)
MN=QP(cmt)
Do đó: MNPQ là hình bình hành
Xét ΔABD có
Q là trung điểm của AD
M là trung điểm của AB
Do đó: QM là đường trung bình của ΔABD
Suy ra: QM//DB và \(QM=\dfrac{DB}{2}\)
hay \(QM=\dfrac{AC}{2}\)(3)
Từ (2) và (3) suy ra QM=QP
Hình bình hành MNPQ có QM=QP(cmt)
nên MNPQ là hình thoi

nè , em đăng bài nhầm đó à , thứ nhất :em lm đề sai / thứ 2 : em đăng muộn qá , ko ai còn on nữa ồi

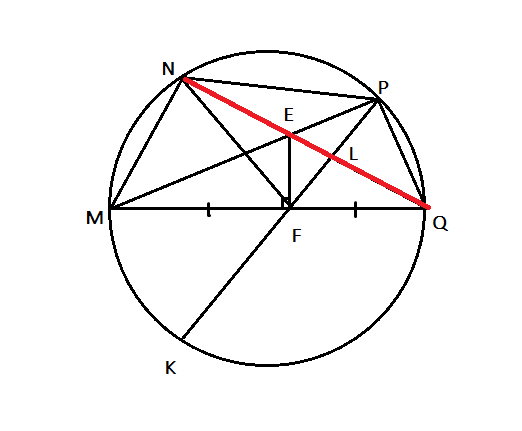
Hình dễ tự vẽ
a ) + b )Ta có \(\widehat{MPQ}=90^o\)( góc nội tiếp chắn nửa đường tròn ) ; \(EF\perp MQ\Rightarrow\widehat{EPQ}+\widehat{EFQ}=90^o+90^o=180^o\)=> tứ giác PEFQ nội tiếp đường tròn đường kính PQ
Tương tự => \(\widehat{ENM}+\widehat{EFM}=90^o+90^o=180^o\)=> tứ giácMNEF nội tiếp => \(\widehat{PFQ}=\widehat{PEQ}\)( hai góc nội tiếp cùng chắn cung PQ trong đường tròn đường kính EQ )
\(\widehat{NFM}=\widehat{NEM}\)( hai góc nội tiếp cùng chắn cung MN trong đường tròn đường kính ME )
\(\widehat{NEM}=\widehat{PEQ}\)( hai góc đối đỉnh ) , \(\widehat{PFQ}=\widehat{MFK}\)( hai góc đối đỉnh )
\(\Rightarrow\widehat{NFM}=\widehat{KFM}\)hay FM là tia phân giác của \(\widehat{NFK}\)
c) Có : \(\widehat{NPM}=\widehat{NQM}\)( hai góc nội tiếp cùng chắn cung MN trong đường tròn đường kính MQ )
\(\widehat{EPF}=\widehat{EQF}\)( hai góc nội tiếp cùng chắn cung EF trong đường tròn đường kính EQ )
\(\Rightarrow\widehat{NPE}=\widehat{EPL}\) => PE là phân giác trong của \(\Delta NPL\). Lại có \(PE\perp PQ\)=> PE là phân giác ngoài của \(\Delta NPL\Rightarrow\frac{EN}{EL}=\frac{QN}{QL}\Rightarrow EN.QL=QN.EL\)(đpcm)

a) Ta có: góc Q =góc P
=> AQ = AP ( quan hệ giữa góc và cạnh đối diện)
Ta có: AM + MQ = AQ
AN + NP = AP
Mà MQ = NP ( MNPQ là hình thang cân).
AQ = AP (cmt)
=> AM = AN => tam giác MAN cân tại A.
Câu b bạn tự làm nha
a.
Xét hai tam giác MNP và MQP có:
\(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\\MP\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta MNP=\Delta MQP\left(c.c.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{NMP}=\widehat{QMP}\\\widehat{NPM}=\widehat{QPM}\end{matrix}\right.\) hay MP là phân giác của góc M và P
b.
Do \(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\end{matrix}\right.\) \(\Rightarrow MP\) là trung trực NQ
\(\Rightarrow MP\perp NQ\) (đpcm)