Nêu điều kiện để tam giác DEF = tam giác GHI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 8 2023
Để hai tam giác trên bằng nhau theo trường hợp c.c.c thì các cặp cạnh tương ứng phải bằng nhau. Vì đã có hai cặp cạnh tương ứng là MN và DE, PM và DF nên cần thêm điều kiện NP = EF để hai tam giác trên bằng nhau theo trường hợp c.c.c
CM
24 tháng 9 2017
Đáp án C
Để tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là: A ^ = D ^
30 tháng 3 2021
vuông tại A, D chứ vuông tại đâu. học toán rùi mà ko biết là sao ?
3 tháng 12 2017
pn tự vẽ hình nhak
a, có MP // DE (GT) suy ra MP // DN ( N thuộc DF )
MN // DF (GT) suy ra MN // DP ( P thuộc DF )
Suy ra tứ giác NMPD là hình bình hành ( dấu hiệu nhận biết các cạnh đối // )
b, ( cm ngược lại nhak )
có tứ giác NMPD là HCN suy ra góc NDB = 90 độ
suy ra tam giác DEF vuông tại D
Vậy nếu tam giác DEF vuông tại D thì tứ giác NMPD là HCN
c, có tứ giác NMPD là HV suy ra DM là tia phân giác của góc D ứng vs cạnh EF
Vậy nếu DM là tia phân giác của góc D thì tứ giác MNPD là HV
<<< mk lm v có j sai sót pn góp ý dùm mk nhak >>>
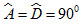
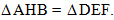
tam giác DEF = tam giác GHI <=> DE = GH ; DF = GI ; EF = HI
góc D = góc G ; góc E = góc H ; góc F = góc I
Tam giac DEF = tam giac GHI <=> DE = GH ,DF = GI,EF = HI
Góc D = góc G,góc E = góc H,góc F = góc I
Bài này dễ mà?