K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PN
1
Những câu hỏi liên quan
NT
0
11 tháng 7 2016
= x3 + 33 -x(x2 -1) -27 =0 ( tổng các lập phuong)
x =0
CX100%
MC
8 tháng 7 2021
\(\frac{22}{9}-\left(x+\frac{1}{2}\right)^2=\frac{7}{3}\)
\(\left(x+\frac{1}{2}\right)^2=\frac{22}{9}-\frac{7}{3}\)
\(\left(x+\frac{1}{2}\right)^2=\frac{1}{9}\)
\(\left(x+\frac{1}{2}\right)^2=\left(\frac{1}{3}\right)^2\)
\(\Rightarrow x+\frac{1}{2}=\frac{1}{3}\)
\(x=\frac{1}{3}-\frac{1}{2}\)
\(x=-\frac{1}{6}\)
DL
8 tháng 7 2021
\(\frac{22}{9}-\left(x+\frac{1}{2}\right)^2=\frac{7}{3}\)
\(\left(x+\frac{1}{2}\right)^2=\frac{22}{9}=\frac{7}{3}\)\
\(\left(x+\frac{1}{2}\right)^2=\frac{22}{9}-\frac{21}{9}\)
\(\left(x+\frac{1}{2}\right)^2=\frac{1}{9}\)
\(\Rightarrow x+\frac{1}{2}=\pm\frac{1}{3}\)
TH1:\(x+\frac{1}{2}=\frac{1}{3}\)
\(x=\frac{1}{3}-\frac{1}{2}\)
\(x=-\frac{1}{6}\)
TH2:\(x+\frac{1}{2}=-\frac{1}{3}\)
\(x=-\frac{1}{3}-\frac{1}{2}\)
\(x=-\frac{5}{6}\)
Vậy \(x\in\left\{-\frac{1}{6};-\frac{5}{6}\right\}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(Bài.1:\\ a,3x-9y=3\left(x-3y\right)\\ b,x^2-5x=x\left(x-5\right)\\ c,\left(x-3\right)\left(x-5\right)-\left(2x+1\right)\left(3-x\right)=\left(x-3\right)\left(x-5\right)+\left(x-3\right)\left(2x+1\right)\\ =\left(x-3\right)\left(x-5+2x+1\right)=\left(x-3\right)\left(3x-4\right)\\ d,3x^3+6x^2+3x=3x\left(x^2+2x+1\right)=3x\left(x+1\right)^2\\ e,3\left(x+5\right)-x^2-5x=3\left(x+5\right)-x\left(x+5\right)\\ =\left(x+5\right)\left(3-x\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(Bài.2:\\ a,x^3-9x=0\\ \Leftrightarrow x.\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\\ b,5x\left(x+2\right)-3\left(x+2\right)=0\\ \Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}5x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-2\end{matrix}\right.\\ c,x^2-7x=0\\ \Leftrightarrow x\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
KV
13 tháng 7 2023
Hiệu của mẫu số và tử số là 26
Tổng của tử số và mẫu số là:
120 × 2 = 240
Tử số là:
(240 - 26) : 2 = 107
Mẫu số là:
107 + 26 = 133
Phân số cần tìm là 107/133
M
0
NT
1
A
2
PL
2
27 tháng 8 2021
Ta có: \(\left(x-3.5\right)^2\ge0\forall x\)
\(\left(y-\dfrac{1}{10}\right)^4\ge0\forall y\)
Do đó: \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(\dfrac{7}{2};\dfrac{1}{10}\right)\)
HV
27 tháng 8 2021
do
\(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\ge0\)
mà ta có \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4\le0\)
nên \(\left(x-3.5\right)^2+\left(y-\dfrac{1}{10}\right)^4=0\)
suy ra \(\left\{{}\begin{matrix}x-3,5=0\\y-\dfrac{1}{10}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3,5\\y=\dfrac{1}{10}\end{matrix}\right.\)
tick mik nha
HN
2
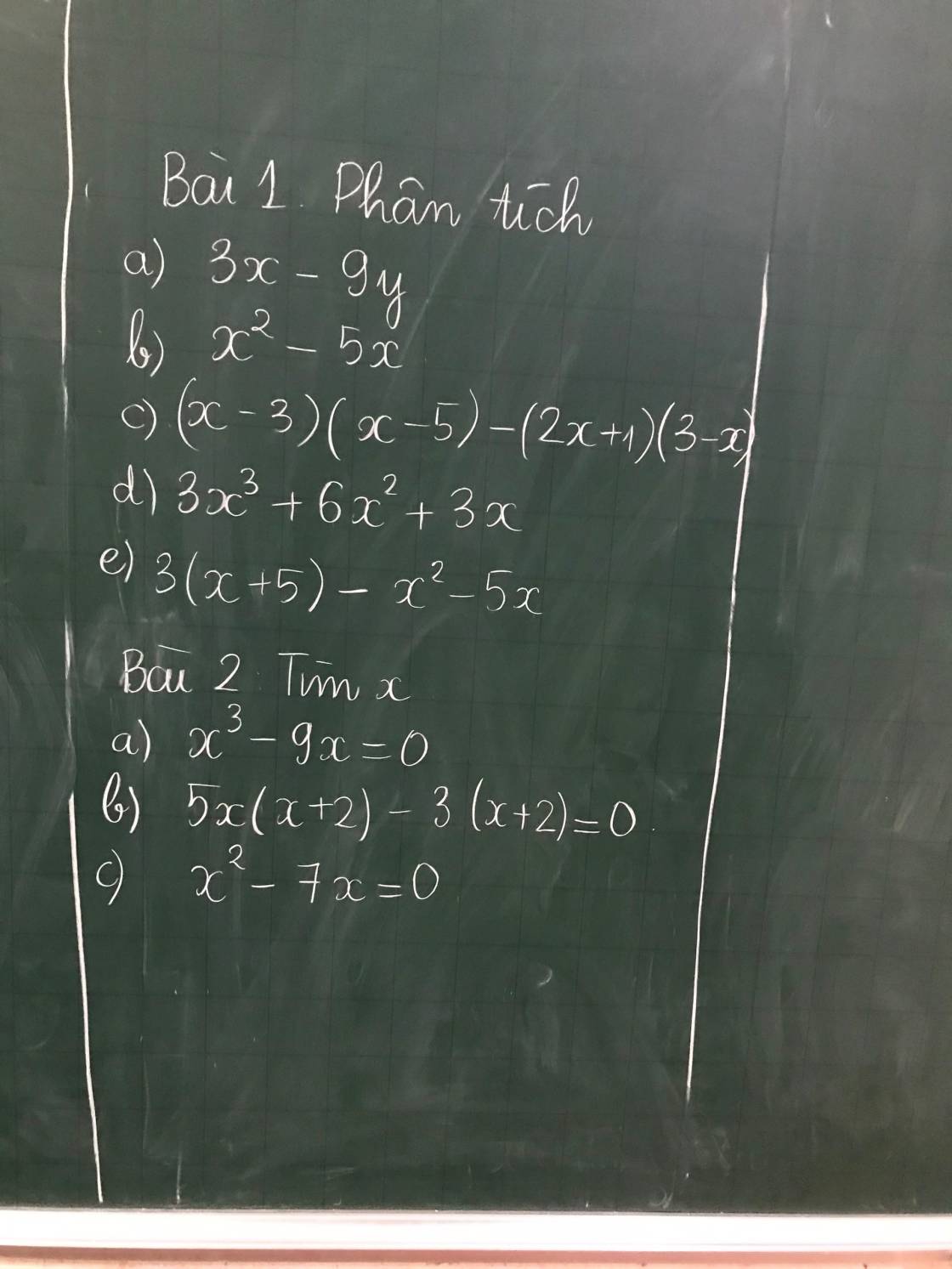
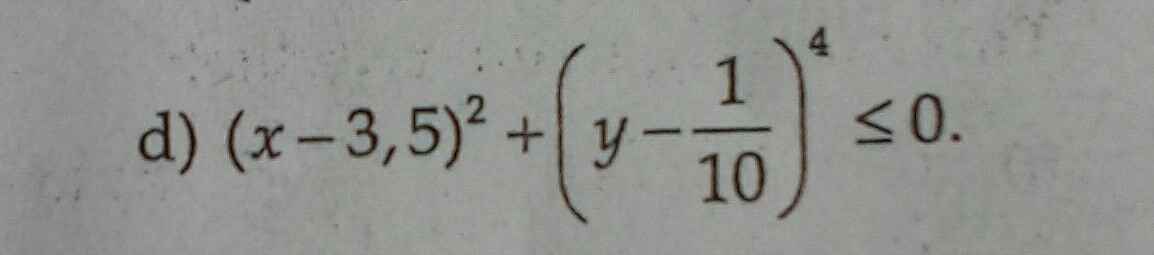
Bài 3 :
a, \(x=3-2\sqrt{2}\Rightarrow\sqrt{x}=\sqrt{3-2\sqrt{2}}=\sqrt{2}-1\)
Thay vào B ta được : \(B=\frac{7}{\sqrt{2}-1+3}=\frac{7}{\sqrt{2}+2}=\frac{7}{\sqrt{2}+2}\)
\(=\frac{7\left(\sqrt{2}-2\right)}{2-4}=-\frac{7\sqrt{2}-14}{2}\)
b, Với \(x\ge0;x\ne25\)
\(A=\frac{6\sqrt{x}}{x-25}-\frac{3}{\sqrt{x}+5}+\frac{4}{\sqrt{x}-5}\)
\(=\frac{6\sqrt{x}-3\left(\sqrt{x}-5\right)+4\left(\sqrt{x}+5\right)}{x-25}\)
\(=\frac{3\sqrt{x}+15+4\sqrt{x}+20}{x-25}=\frac{7\sqrt{x}+35}{x-25}=\frac{7}{\sqrt{x}-5}\)
Ta có : \(M=\frac{A}{B}=\frac{7}{\sqrt{x}-5}.\frac{\sqrt{x}+3}{7}=\frac{\sqrt{x}+3}{\sqrt{x}-5}\)
c, \(M< \frac{1}{2}\Rightarrow\frac{\sqrt{x}+3}{\sqrt{x}-5}-\frac{1}{2}< 0\)
\(\Leftrightarrow\frac{2\sqrt{x}+6-\sqrt{x}+5}{2\sqrt{x}-10}< 0\Leftrightarrow\frac{\sqrt{x}+11}{2\sqrt{x}-10}< 0\)
\(\Rightarrow\sqrt{x}-5< 0\Leftrightarrow x< 25\)
Kết hợp với đk vậy 0 =< x < 25