Thế nào là : "Hai góc cùng phụ với 1 góc thứ 3"
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


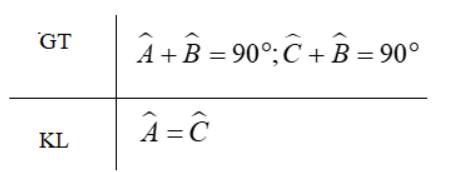
Giả sử \(\widehat A,\widehat C\) cùng phụ với \(\widehat B\). Ta được:
\(\widehat A + \widehat B = 90^\circ ;\widehat C + \widehat B = 90^\circ \)
\(\widehat A = 90^\circ - \widehat B;\widehat C = 90^\circ - \widehat B\)
\( \Rightarrow \widehat A = \widehat C\) (đpcm)

1 góc kề bù là góc vừa kề nhau vừa bù nhau
2 hai góc phụ nhau là 2 góc có tổng số đo là 90 '
3 hai góc kề nhau là 2 góc có 1 cạnh chung và 2 cạnh còn lại nằm trên 2 nửa mặt phẳng đối nhau có bờ chứa canh chung
4 hai góc bù nhau là 2 góc có tỏng số đo là 180 '
mik bổ sung cho bạn Học nữa học mãi cố gắng học . Ng Mai 6a ^-^ nhé:
1. Góc kề bù có tổng số đo là 180o

trl:* tham khảo*
Góc bù nhau là 2 góc có tổng bằng 180 độ
Góc kề bù là hai góc kề nhau có tổng bằng 180 độ
Gó phụ nhau là có tổng hai góc bằng 90 độ
Gó kề nhau có tổng bằng 180 độ
và tổng hai góc phụ nhau bằng 90 đô
1. là 2 góc có tổng số đo = 180o
2. là 2 góc sát nhau
3. là 2 góc sát nhau có tổng số đo là 90o
4. là 2 góc vừa kề vừa bù
đúng ko mn

1) 2 góc kề bù là : hai góc vừa kề nhau vừa bù nhau
2) 2 góc phụ nhau là : là hai góc có tổng số đo = 90 độ, VD : góc 40 độ và góc 50 độ
3) 2 góc kề nhau là : hai góc hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung
4) 2 góc bù nhau là : hai góc có tổng số đo bằng 180 độ VD : góc 120 độ và góc 60 độ
Ủng hộ mik nha

Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)

Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |

vẽ hình hai góc cùng phụ vói một góc thứ ba thì bằng nhau
2 goc cong lai bang 180 do
Thế 2 góc cùng phụ vs 1 góc thứ 3 thì bằng nhau nghĩa là j?