Cho hình chữ nhật ABCD(Có 4 góc vuông);AB>AD. CMR: phân giác của góc D và góc B song song với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 2 2018
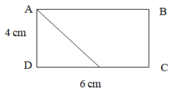
a) Hình bên có: 4 góc vuông, 3 góc nhọn, 1 góc tù.
b) Chu vi hình chữ nhật ABCD là : (4+6) x 2 = 20 cm.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
b.
Từ câu a ta có \(AB\perp\left(SAD\right)\)
Mà \(SD\in\left(SAD\right)\)
\(\Rightarrow AB\perp SD\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
Gọi M là trung điểm AD \(\Rightarrow OM\perp AD\Rightarrow OM\perp\left(SAD\right)\)
\(\Rightarrow\widehat{MSO}\) là góc giữa SO và (SAD)
\(SM=\sqrt{SA^2+\left(\dfrac{AD}{2}\right)^2}=2\sqrt{2}\)
\(OM=\dfrac{1}{2}CD=1\)
\(tan\widehat{MSO}=\dfrac{OM}{SM}=\dfrac{1}{2\sqrt{2}}\) \(\Rightarrow\widehat{MSO}\approx19^028'\)
LT
26 tháng 3 2015
Bài này mà của lớp 9 thì dễ, lớp 8 thì làm thế này nhé.
Trên AD lấy điểm E sao cho góc ABE=60 độ.
Đặt AB = x (x>0)
Tam giác ABE vuông có góc ABE = 60 độ nên BE = 2 AB = 2x.
Áp dụng định lí Pi-ta-go => AE= \(\sqrt{3}\)x
Tam giác BED cân tại E => BE = ED = 2x.
=> AD = AE + ED =\(\sqrt{3}\)x +2x =x(\(\sqrt{3}\) +2)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD
BD2 = AB2 + AD2 <=> 172 = x2 +(\(\sqrt{3}\)+2)2 x2 => x=\(\frac{17}{\sqrt{8+4\sqrt{3}}}\)
=> AB, AD => Diện tích của hcn ABCD.
CM
28 tháng 3 2017
- AB và BC là một cặp cạnh vuông góc với nhau.
- BC và CD là một cặp cạnh vuông góc với nhau
- CD và DA là một cặp cạnh vuông góc với nhau.
- DA và AB là một cặp cạnh vuông góc với nhau.
CM
30 tháng 5 2018
- AB và BC là một cặp cạnh vuông góc với nhau.
- BC và CD là một cặp cạnh vuông góc với nhau
- CD và DA là một cặp cạnh vuông góc với nhau.
- DA và AB là một cặp cạnh vuông góc với nhau.
A B C D x y 1 1 H
Vì x là phân giác của D
=> D1 = D2 = D/2 = 90/2 = 45
Vì y là phân giác của B
=> B1 = B2 = B/2 = 90/2 = 45
Áp dụng tổng 3 góc của một tam giác , ta có :
B1 + H + C = 180
mà B1 = 45 ; C = 90
=> 45 + 90 + H = 180
=> H = 45
Vì H = D1
mà 2 góc nằm ở vị trí đồng vị
=> Dx//By ( điều phải chứng minh)