- - Chứng minh rằng: 2√2 (√3 - 2) + (1 + 2√2)2 - 2√6 = 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PL
2
Những câu hỏi liên quan
3 tháng 9 2017
a>
\(\frac{1}{2^2}+\frac{1}{100^2}\)=1/4+1/10000
ta có 1/4<1/2(vì 2 đề bài muốn chứng minh tổng đó nhỏ 1 thì chúng ta phải xét xem có bao nhiêu lũy thừa hoặc sht thì ta sẽ lấy 1 : cho số số hạng )
1/100^2<1/2
=>A<1
VY
0
PN
1
H9
HT.Phong (9A5)
CTVHS
10 tháng 11 2023
Ta có:
\(\dfrac{1}{2^2}=\dfrac{1}{2\cdot2}< \dfrac{1}{1\cdot2}\)
\(\dfrac{1}{3^2}=\dfrac{1}{3\cdot3}< \dfrac{1}{2\cdot3}\)
\(\dfrac{1}{4^2}=\dfrac{1}{4\cdot4}< \dfrac{1}{3\cdot4}\)
...
\(\dfrac{1}{9^2}=\dfrac{1}{9\cdot9}< \dfrac{1}{8\cdot9}\)
\(\dfrac{1}{10^2}=\dfrac{1}{10\cdot10}< \dfrac{1}{9\cdot10}\)
\(\Rightarrow A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{10^2}< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{9\cdot10}\)
\(\Rightarrow A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(\Rightarrow A< 1-\dfrac{1}{10}\)
\(\Rightarrow A< \dfrac{9}{10}\)
\(\Rightarrow A< 1\) (vì: \(\dfrac{9}{10}< 1\))
VT
Vũ thị Tình
VIP
10 tháng 11 2023
221=2⋅21<1⋅21
132=13⋅3<12⋅3321=3⋅31<2⋅31
142=14⋅4<13⋅4421=4⋅41<3⋅41
...
192=19⋅9<18⋅9921=9⋅91<8⋅91
1102=110⋅10<19⋅101021=10⋅101<9⋅101
⇒�=122+132+142+...+1102<11⋅2+12⋅3+13⋅4+...+19⋅10⇒A=221+321+421+...+1021<1⋅21+2⋅31+3⋅41+...+9⋅101
⇒�<1−12+12−13+...+19−110⇒A<1−21+21−31+...+91−101
⇒�<1−110⇒A<1−101
⇒�<910⇒A<109
⇒�<1⇒A<1 (vì: 910<1109<1)
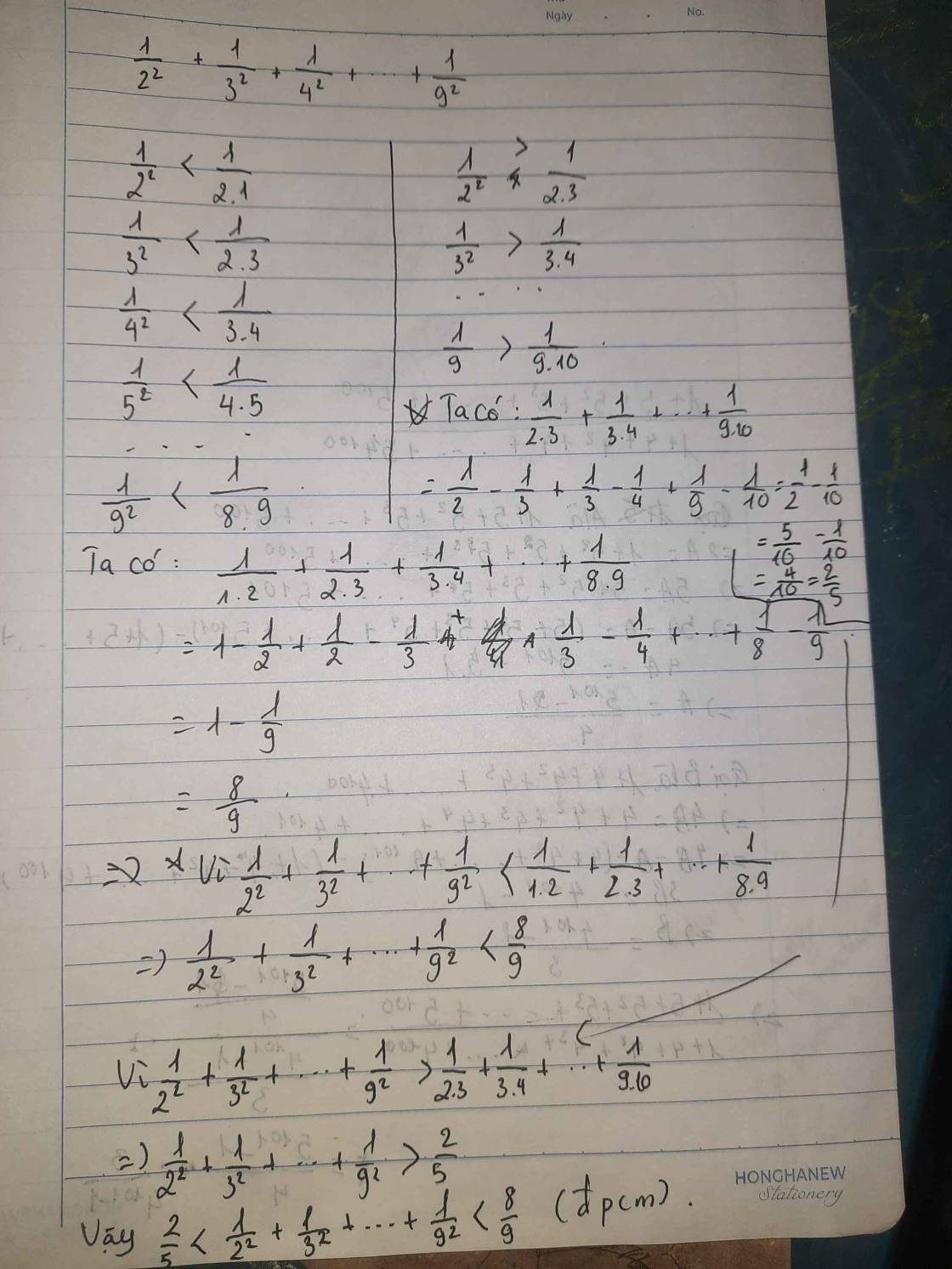
de sai ak
@Nguyễn Huy Thắng Đề k sai, mình chứng minh được rồi -.-