Cho 3 đường thẳng xx'; yy'; zz' cắt nhau tại O
CMR: tồn tại ít nhất 1 góc có đỉnh O không \(\le60^o\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho 3 đường thẳng xx'; yy'; zz' cắt nhau tại O
CMR: tồn tại ít nhất 1 góc có đỉnh O không \(\le60^o\)


– TH1: M ∈ Ot
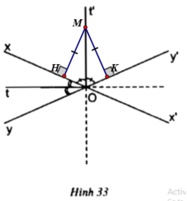
M ∈ Ot do Ot là phân giác của 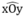 nên M cách đều hai tia Ox và Oy
nên M cách đều hai tia Ox và Oy
⇒ M cách đều xx’, yy’.
Tương tự cho M thuộc tia đối của tia Ot.
- TH2: M ∈ Ot’
M ∈ Ot’ do Ot’ là phân giác của 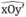 nên M cách đều hai tia Ox, Oy’
nên M cách đều hai tia Ox, Oy’
⇒ M cách đều xx’, yy’.
Tương tự cho M thuộc tia đối của tia Ot’.
Vậy với mọi M thuộc đường thẳng Ot hoặc đường thẳng Ot’, M cách đều xx’ và yy’.

Ta có M luôn thuộc miền trong của một trong bốn góc:
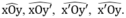
Mà M cách đều xx’ và yy’ nên theo định lý 2 ta có:
+ Nếu M thuộc miền trong góc xOy ⇒ M thuộc tia Ot.
+ Nếu M thuộc miền trong góc xOy’ ⇒ M thuộc tia Ot’.
+ Nếu M thuộc miền trong góc y’Ox’ ⇒ M thuộc tia đối của tia Ot.
+ Nếu M thuộc miền trong góc x’Oy ⇒ M thuộc tia đối của tia Ot’ .

Ta có M luôn thuộc miền trong của một trong bốn góc:
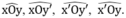
Mà M cách đều xx’ và yy’ nên theo định lý 2 ta có:
+ Nếu M thuộc miền trong góc xOy ⇒ M thuộc tia Ot.
+ Nếu M thuộc miền trong góc xOy’ ⇒ M thuộc tia Ot’.
+ Nếu M thuộc miền trong góc y’Ox’ ⇒ M thuộc tia đối của tia Ot.
+ Nếu M thuộc miền trong góc x’Oy ⇒ M thuộc tia đối của tia Ot’ .
Giả sử trong 3 đường thẳng xx'; yy'; zz' cắt nhau tại O không tồn tại góc đỉnh O \(\le60^o\) (tức là tất cả các không có điểm trong chung > 60o)
Trong 3 đường thẳng cắt nhau tại O sẽ tạo ra 6 góc không có điểm trong chung
=> tổng các góc đó > 6.60o = 360o (vô lý vì tổng các góc = 360o)
=> điều giả sử là sai
Vậy trong 3 đường thẳng cắt nhau tồn tại ít nhất 1 góc có đỉnh O không \(\le60^o\)