\(\overrightarrow{MN}=k\overrightarrow{PQ}\)\(\Rightarrow\)MN song song với PQ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
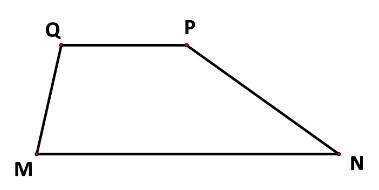
Do MQ và PN không song song với nhau nên \(\overrightarrow {MQ} \ne k\overrightarrow {NP} \). Vậy loại B và D.
Ta có: \(\overrightarrow {MN} ,\overrightarrow {PQ} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
Vậy chọn C.
HQ
23 tháng 7 2019
Dễ mà bạn :)) cái này dùng qui tắc công với chèn điểm là nuột =)
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{MN}\)
\(=\overrightarrow{NQ}+\overrightarrow{MN}=\overrightarrow{MN}+\overrightarrow{NQ}=\overrightarrow{MQ}\left(đpcm\right)\)
( quá chi tiết rồi nha bạn... )
b) Ta có: \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{QN}\)
\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{NQ}+\overrightarrow{QN}\)
\(\Rightarrow\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\left(đpcm\right)\)
BT
12 tháng 5 2017
TenAnh1
TenAnh1
A = (-4, -6.26)
A = (-4, -6.26)
A = (-4, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).
3 tháng 8 2023
a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân
