Câu 1 : Vẽ xMy và xNz ở vị trí đồng vị và = 130 độ . Hỏi có 2 đường thẳng nào song song ko . vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 9 2016
Áp dụng tính chất: Nếu 2 đường thẳng song song với nhau thì 2 góc so le trong = nhau
19 tháng 8 2016
Gọi an là số miền do n đường thẳng thỏa bài toán sinh ra.
Xét nn đường thẳng d1,d2,.....,dn cắt nhau tạo thành an miền, đường thẳng dn+1 cắt tất cả các đường thẳng trên và bị n đường thẳng trên chia thành n+1 phần với mỗi miền đó sẽ tại ra một miền cũ và một miền mới.
Ta có an+1=an+n+1
Giải phương trình sai phân này ta được \(a_n=\frac{n^2+n+2}{2}\)tức là \(\frac{n^2+n+2}{2}\)miền.
19 tháng 8 2016
Gọi \(a_n\) là số miền do \(n\) đường thẳng ( giả thiết ) chia ra .
Xét \(n\) đường thẳng \(d_1;\) \(d_2;...\)\(;d_{n-1};\)\(d_n\)cắt nhau tạo thành \(a_n\) miền, đường thẳng \(d_{n+1}\) đi qua các đường thẳng trên và bị \(n\) đường thẳng nó đi qua chia thành \(n+1\) phần với mỗi miền đó sẽ tại ra một miền cũ và một miền mới.
Ta có :
\(a_{n+1}=a_n+\left(n+1\right)\)
Giải phương trình sai phân này ta được \(a_n=\frac{n^2+n+2}{2}\)tức \(\frac{n^2+n+2}{2}\)miền.
CM
16 tháng 9 2019
Tương tự 1A
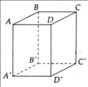
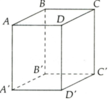
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')
8 tháng 1 2024
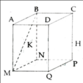
a: Xét ΔAME và ΔADC có
\(\widehat{AME}=\widehat{ADC}\)(hai góc đồng vị, ME//DC)
\(\widehat{MAE}\) chung
Do đó: ΔAME đồng dạng với ΔADC
=>\(\dfrac{AM}{AD}=\dfrac{ME}{DC}=\dfrac{AE}{AC}=\dfrac{1}{3}\)
Xét ΔCEN và ΔACD có
\(\widehat{CEN}=\widehat{ACD}\)(hai góc so le trong, EN//CD)
\(\widehat{ECN}=\widehat{CAD}\)(hai góc so le trong, CN//AD)
Do đó: ΔCEN đồng dạng với ΔACD
=>\(\dfrac{CE}{AC}=\dfrac{EN}{CD}=\dfrac{CN}{AD}=\dfrac{2}{3}\)
b: E là trung điểm của MN
=>EM=EN
Xét ΔEAM và ΔECN có
\(\widehat{EAM}=\widehat{ECN}\)(hai góc so le trong, AM//CN)
\(\widehat{AEM}=\widehat{CEN}\)(hai góc đối đỉnh)
Do đó: ΔEAM đồng dạng với ΔECN
=>\(\dfrac{EA}{EC}=\dfrac{EM}{EN}=1\)
=>E là trung điểm của AC
CM
27 tháng 10 2017
* Góc đồng vị với A 1 ^ bằng 30o, khác A 1 ^ nên b1 không song song với a.
Vậy b1 không trùng với b.
* Góc kề bù với góc đồng vị của A 1 ^ bằng 145o nên góc
đồng vị với A 1 ^ bằng 180o – 145o = 35o = A 1 ^ .
Vậy b2 song song với a nên b2 trùng với b (theo tiên đề Ơ-clit)
CM
24 tháng 3 2019
a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').
2 tháng 12 2021
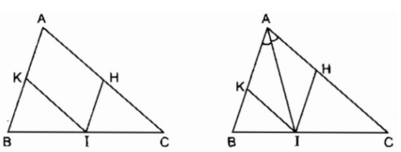
a, Vì \(HI\text{//}AB;KI\text{//}AC\Rightarrow AHIK\text{ là hbh}\)
b, Để \(AHIK\) là hình thoi thì \(AI\) là phân giác \(\widehat{HIK}\)
Hay I là chân đường phân giác từ A tới BC
c, Để \(AHIK\) là hcn thì \(\widehat{HAK}=90^0\) hay \(\widehat{BAC}=90^0\)
Vậy tam giác ABC vuông tại A thì \(AHIK\) là hcn
CM
10 tháng 10 2019
Hình bình hành AHIK là hình thoi nên đường chéo AI là phân giác của ∠ (BAC)
Ngược lại nếu AI là phân giác của ∠ (BAC) thì hình bình hành AHIK có đường chéo AI là phân giác của một góc nên hình bình hành AHIK là hình thoi.
Vậy nếu I là giao điểm của đường phân giác của ∠ A với cạnh BC thì tứ giác AHIK là hình thoi.
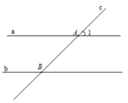
ngoài 2 đường thẳng MY và NZ thì ko có 2 đường thẳng nào song song vì theo tiên đề ơ clits :Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
M N x y z 130 130