Nghiệm nguyên nhỏ nhất của bất phương trình là
....
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TN
3

Những câu hỏi liên quan

CM
24 tháng 11 2017

Vậy nghiệm nguyên nhỏ nhất của phương trình đã cho là: x = 17.
Chọn D

CM
9 tháng 10 2019
Điều kiện: x > 2
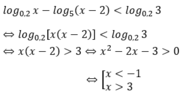
So điều kiện suy ra x > 3
Vậy nghiệm nguyên nhỏ nhất của bất phương trình đã cho là x = 4
Chọn A

CM
10 tháng 10 2017
Điều kiện: x > 2
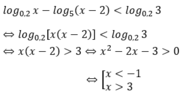
So điều kiện suy ra x > 3
Vậy nghiệm nguyên nhỏ nhất của bất phương trình đã cho là x = 4
Chọn A
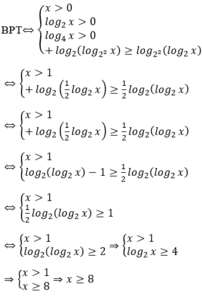
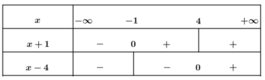
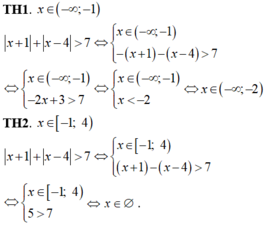

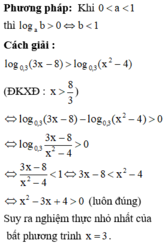

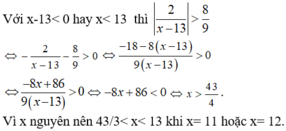
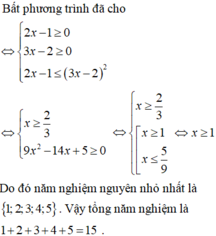

Điều kiện : \(x\ge-1\)
Bình phương hai vế : \(x+1< \left(x+3\right)^2\Leftrightarrow x^2+6x+9>x+1\Leftrightarrow x^2+5x+8>0\)
Mà \(x^2+5x+8=\left(x+\frac{5}{2}\right)^2+\frac{7}{4}>0\) với mọi x
Vậy : nghiệm nguyên nhỏ nhỏ nhất của x bằng -1
\(\sqrt{x+1}< x+3\)
<=> \(\begin{cases}x+1\ge0\\x+3\ge0\\x+1< x^2+6x+9\end{cases}\)
<=> \(\begin{cases}x\ge-1\\x^2+5x+8>0\end{cases}\)
<=> \(\begin{cases}x\ge-1\\x\in R\end{cases}\)
=> x>=-1
=> Nghiệm NN là -1