6sinx-2cos^3x=5sin2xcosx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LL
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2020
a/
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(3tan^3x+2tan^2x=tanx\)
\(\Leftrightarrow tanx\left(3tan^2x+2tanx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=0\\3tan^2x+2tanx-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=0\\tanx=-1\\tanx=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=-\frac{\pi}{4}+k\pi\\x=arctan\left(\frac{1}{3}\right)+k\pi\end{matrix}\right.\)
b/ \(\Leftrightarrow3sinx+cos^3x=5sinx.cos^2x\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(3tanx.\frac{1}{cos^2x}+1=5tanx\)
\(\Leftrightarrow3tanx\left(1+tan^2x\right)-5tanx+1=0\)
\(\Leftrightarrow3tan^3x-2tanx+1=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(3tan^2x-3tanx+1\right)=0\)
\(\Leftrightarrow tanx=-1\Rightarrow x=-\frac{\pi}{4}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2020
b/ ĐKXĐ: \(cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
\(6sinx-2cos^3x=\frac{10sin2x.cos2x.sinx}{2cos2x}\)
\(\Leftrightarrow6sinx-2cos^3x=5sin2x.sinx\)
\(\Leftrightarrow3sinx-cos^3x=5cosx.sin^2x\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(3tanx\left(1+tan^2x\right)-1=5tan^2x\)
\(\Leftrightarrow3tan^3x-5tan^2x+3tanx-1=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(3tan^2x-2tanx+1\right)=0\)
\(\Leftrightarrow tanx=1\Rightarrow x=\frac{\pi}{4}+k\pi\) (ko thỏa mãn ĐKXĐ)
Vậy pt vô nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2020
d/
\(\Leftrightarrow\left(cos^2x-sin^2x\right)\left(sinx+cosx\right)-4cos^3x\left(sin^2x+cos^2x+2sinx.cosx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(sinx+cosx\right)^2-4cos^3x\left(sinx+cosx\right)^2=0\)
\(\Leftrightarrow\left(cosx-sinx-4cos^3x\right)\left(sinx+cosx\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\cosx-sinx-4cos^3x=0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=0\Leftrightarrow x+\frac{\pi}{4}=k\pi\)
\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)
Xét \(\left(2\right)\), nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow\frac{1}{cos^2x}-tanx.\frac{1}{cos^2x}-4=0\)
\(\Leftrightarrow1+tan^2x-tanx\left(1+tan^2x\right)-4=0\)
\(\Leftrightarrow-tan^3x+tan^2x-tanx-3=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(tan^2x-2tanx+3\right)=0\)
\(\Leftrightarrow tanx=-1\Rightarrow x=-\frac{\pi}{4}+k\pi\)
CM
8 tháng 8 2019
Đáp án A
Đặt 
Yều cẩu bào toán trở thành: Tìm m để bất phương trình 
nghiệm đúng với mọi 
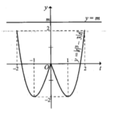
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số 
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là 
HY
0
NT
0
NM
0
6sinx−2cos3x=5sin2xcosx
⇔6sinx−2cos3x=10sinxcos2x
⇔3sinx−cos3x=5sinxcos2x
⇔3sinx(sin2x+cos2x)−cos3x=5sinxcos2x
⇔3sin3x−2sinxcos2x−cos3x=0
Do cosx=0 ko phải là nghiệm của pt nên ta chia cả 2 vế của pt cho cos2x....Khi đó ta được pt tương đương:
⇔3tan3x−2tanx−1=0⇔(tanx−1)(3tan2x+3tanx+1)=0
đến đây bạn cho từng cái bằng 0 là giải ra được
bài của mình là
6sinx-2cos^3x=5sin2xcosx
chứ không phải là
6sinx cos3
x=5sin2xcosx