Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Qua C kẻ đường thẳng song với PQ, cắt AB tại N, cắt AH tại K
HP=HQ
=>KN=KC
=>KM là đường trung bình của ΔCBN
=>KM//NB
=>KM vuông góc CH
M là trực tâm của ΔCHK
=>HM vuông góc nC
=>HM vuông góc PQ
Bạn tự vẽ hình nha!!!
a.)Xét\(\Delta ABD\)và\(\Delta ABM\)có:
\(AD=BM\)
\(AB:\)Chung
\(\widehat{DAB}=\widehat{ABM}\left(slt\right)\)
\(\Rightarrow\Delta ABD=\Delta BAM\)
b.)Ta có:\(\Delta ABD=\Delta BAM\)(Theo a)
\(\Rightarrow\widehat{DBA}=\widehat{BAM}\)(mà 2 góc SLT)
\(\Rightarrow AM//BD\)
c.)Xét\(\Delta ADI\)và\(\Delta IMC\)có:
\(AD=CM\)
\(\widehat{DAI}=\widehat{IMC}\)
\(AI=IM\)
\(\Rightarrow\Delta AID=\Delta IMC\)
\(\Rightarrow IA=IC\)
\(\Rightarrow I\)là trung điểm của\(AC\)
\(\Rightarrow I,A,C\)thẳng hàng(đpcm)
P/s:#Study well#
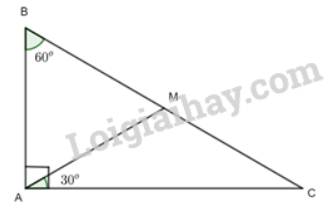
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
A B C M D H I
a) Bạn nối điểm A với M trên hình vẽ giúp mình nhé, mình quên chưa vẽ...
Xét \(\Delta ABM,\Delta ACM\) có :
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{ABM}=\widehat{ACM}\left(gt\right)\\BM=MC\left(\text{M là trung điểm của BC}\right)\end{matrix}\right.\)
=> \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
=> \(\widehat{BAM}=\widehat{ACM}\) ( 2 góc tương ứng)
Xét \(\Delta ABH,\Delta CAI\) có :
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{AHB}=\widehat{CIA}=90^o\\\widehat{BAH}=\widehat{ACI}\left(=90^o-\widehat{IAC}\right)\end{matrix}\right.\)
=> \(\Delta ABH=\Delta CAI\left(ch-gn\right)\)
=> BH = AI (2 cạnh tương ứng)
