cho x+2y=5. CMR: x2+y2>5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BD
0
25 tháng 5 2016
Áp dụng BĐT Bunhiacopxky ta có :
( x + 2y )2 <= ( 12 + 22 )( x2 + y2 )
52 <= 5( x2 + y2 )
5( x2 + y2 ) >= 25
x2 + y2 >= 25/5
x2 + y2 >= 5
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)
\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)
\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
Lời giải:
a.
$x^2-x=y^2-1$
$\Leftrightarrow x^2-x+1=y^2$
$\Leftrightarrow 4x^2-4x+4=4y^2$
$\Leftrightarrow (2x-1)^2+3=(2y)^2$
$\Leftrightarrow 3=(2y)^2-(2x-1)^2=(2y-2x+1)(2y+2x-1)$
Đến đây xét các TH:
TH1: $2y-2x+1=1; 2y+2x-1=3$
TH2: $2y-2x+1=-1; 2y+2x-1=-3$
TH3: $2y-2x+1=3; 2y+2x-1=1$
TH4: $2y-2x+1=-3; 2y+2x-1=-1$
b.
$x^2+12x=y^2$
$\Leftrightarrow (x+6)^2=y^2+36$
$\Leftrightarrow 36=(x+6)^2-y^2=(x+6-y)(x+6+y)$
Đến đây xét trường hợp tương tự phần a.
c.
$x^2+xy-2y-x-5=0$
$\Leftrightarrow x^2+xy=x+2y+5$
$\Leftrightarrow 4x^2+4xy=4x+8y+20$
$\Leftrightarrow (2x+y)^2=4x+8y+20+y^2$
$\Leftrightarrow (2x+y)^2-2(2x+y)+1=y^2+6y+21$
$\Leftrightarrow (2x+y-1)^2=(y+3)^2+12$
$\Leftrightarrow (2x+y-1)^2-(y+3)^2=12$
$\Leftrightarrow (2x+y-1-y-3)(2x+y-1+y+3)=12$
$\Leftrightarrow (2x-4)(2x+2y+2)=12$
$\Leftrightarrow (x-2)(x+y+1)=3$
Đến đây đơn giản rồi.
8 tháng 8 2021
a) \(x^2-x=y^2-1\)
\(\Rightarrow x^2-x+1=y^2\)
\(\Rightarrow4x^2-4x+4=4y^2\)
\(\Rightarrow4x^2-4x+1+3=\left(2y\right)^2\)
\(\Rightarrow\left(2x+1\right)^2-\left(2y\right)^2=-3\)
\(\Rightarrow\left(2x-2y+1\right)\left(2x+2y+1\right)=-3\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}\left(2x-2y+1\right)\left(2x+2y+1\right)\in Z\\\left(2x-2y+1\right)\left(2x+2y+1\right)\inƯ\left(7\right)\end{matrix}\right.\)
Ta có bảng:
| x-y | -1 | 0 | -2 | 1 |
| x+y | 1 | -2 | 0 | -1 |
| x | 0 | -1 | -1 | 0 |
| y | 1 | -1 | -1 | -1 |
Vậy \(\left(x,y\right)\in\left\{\left(0;1\right);\left(-1;-1\right);\left(-1;-1\right);\left(0;-1\right)\right\}\)
28 tháng 7 2023
a: =x^3+8-1+27x^3=28x^3+7
b: Sửa đề: (2+y)(y^2-2y+4)+(5-y)(25+5y+y^2)
=8+y^3+125-y^3
=133
CM
21 tháng 3 2017
Các phương trình song song với ∆: x+2y-5=0 có dạng d: x+2y+c=0
Từ đường tròn (C) ta có tâm I(-2;1) và bán kính R=3
Vì đường thẳng d là tiếp tuyến của đường tròn (C) nên ta có:
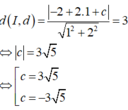
Vậy hai phương trình tiếp tuyến của đường tròn (C) là: x + 2 y + 3 5 = 0 và x + 2 y - 3 5 = 0 .
Áp dụng BĐT Bunhiacopxky ta có :
﴾ x + 2y ﴿^2 <= ﴾ 1^2 + 2^2 ﴿﴾ x^2 + y^2 ﴿
5^2 <= 5﴾ x^2 + y^2 ﴿
5﴾ x^2 + y^2 ﴿ >= 25
x^2 + y^2 >= 25/5
x^2 + y^2 >= 5
M=x^2/xy+y^2/xy Dk xy khac 0
M= x/y + y/x
2M= 2x/y + 2y/x
2M= 2.x/y + (-x +2y+x)/x
2M= 2. (x-2y)/y + 2.2y/x - (x-2y)/x+x/x => 2M=2(x-2y)/y -(x-2y)/x +5
Vi x-2y>=0=>2(x-2y)/y -(x-2y)/x +5>=5
=> 2M>=5
=> M>5/2
vay GTNN cua M=5/2