Giải giúp mình câu 3, 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
0
DQ
1
8 tháng 4 2022
Câu 4:
Thay x=2 và y=-1 vào hệ, ta được:
\(\left\{{}\begin{matrix}2a-b=4\\2b+2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\a=1\end{matrix}\right.\)
PN
0
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 5 2021
Trong mp đáy, qua B kẻ đường thẳng song song AC, lần lượt cắt DA và DC kéo dài tại E và F
\(\Rightarrow AC||\left(SEF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SEF\right)\right)=d\left(A;\left(SEF\right)\right)\)
Gọi I là giao điểm AC và BD
Theo định lý Talet: \(\dfrac{ID}{IB}=\dfrac{DC}{AB}=3\Rightarrow\dfrac{ID}{BD}=\dfrac{3}{4}\)
Cũng theo Talet: \(\dfrac{DA}{DE}=\dfrac{DI}{DB}=\dfrac{3}{4}\Rightarrow AD=\dfrac{3}{4}DE\Rightarrow AE=\dfrac{1}{4}DE\)
\(\Rightarrow d\left(A;\left(SEF\right)\right)=\dfrac{1}{4}d\left(D;\left(SEF\right)\right)\)
Trong tam giác vuông EDF, kẻ \(DH\perp EF\) , trong tam giác vuông SDH, kẻ \(DK\perp SH\)
\(\Rightarrow DK\perp\left(SEF\right)\Rightarrow DK=d\left(D;\left(SEF\right)\right)\)
\(DE=\dfrac{4}{3}AD=\dfrac{4a}{3}\); \(DF=\dfrac{4}{3}DC=4a\)
\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{5}{8a^2}\)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{DH^2}=\dfrac{1}{48a^2}+\dfrac{5}{8a^2}\Rightarrow DK=\dfrac{4a\sqrt{93}}{31}\)
\(\Rightarrow d\left(AC;SB\right)=\dfrac{1}{4}DK=\dfrac{a\sqrt{93}}{31}\)
PH
2
H
15 tháng 3 2023
`3/4-(2/3+3/4)+2/3+2022/2023`
`=3/4 - 2/3 - 3/4 +2/3 +2022/2023`
`= (3/4 -3/4 ) + (-2/3 +2/3) +2022/2023`
`= 0+0+2022/2023`
`=2022/2023`
NK
15 tháng 3 2023
\(\dfrac{3}{4}-\left(\dfrac{2}{3}+\dfrac{3}{4}\right)+\dfrac{2}{3}+\dfrac{2022}{2023}\)
\(=\dfrac{3}{4}-\left(\dfrac{8}{12}+\dfrac{9}{12}\right)+\dfrac{2}{3}+\dfrac{2022}{2023}\)
\(=\dfrac{3}{4}-\dfrac{17}{12}+\dfrac{2}{3}+\dfrac{2022}{2023}\)
\(=\dfrac{9}{12}-\dfrac{17}{12}+\dfrac{8}{12}+\dfrac{2022}{2023}\)
\(=\dfrac{9-17+8}{12}+\dfrac{2022}{2023}=\dfrac{0}{12}+\dfrac{2022}{2023}=0+\dfrac{2022}{2023}\)
\(=\dfrac{2022}{2023}\)
#YTVA
GIẢI GIÚP MÌNH CÂU 4 CẢM ƠN Ạ :3
NV
18 tháng 3 2023
CÂU 4:
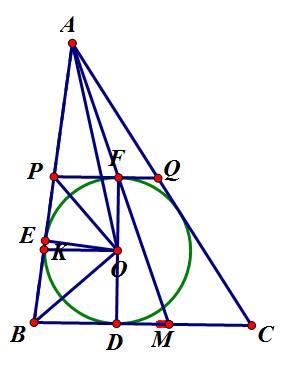
a) △ABC có (O) là tâm đường tròn nội tiếp và (O) tiếp xúc với AB,BC lần lượt tại D,E.
⇒OD⊥BC tại D, OE⊥AB tại E nên \(\widehat{ODB}=\widehat{OEB}=90^0\)
Tứ giác BDOE có \(\widehat{ODB}+\widehat{OEB}=90^0+90^0=180^0\)
\(\Rightarrow\)BDOE là tứ giác nội tiếp.
\(\Rightarrow\)B,D,O,E cùng thuộc 1 đường tròn.
b) Cách đơn giản nhất: *Gọi K là trung điểm BP.
Xét (O): BE, BD là 2 tiếp tuyến cắt nhau ở B.
\(\Rightarrow BE=BD\left(1\right)\)
PF, PE là 2 tiếp tuyến cắt nhau ở P.
\(\Rightarrow PF=PE\left(2\right)\)
Lấy (1)+(2) ta được \(BD+PF=BP\)
Ta có: DF⊥PQ tại F, DF⊥BC tại D nên PQ//BC.
Xét hình thang BDFP (BD//PF) có:
O là trung điểm DF, K là trung điểm BP.
\(\Rightarrow\)KO là đường trung bình của hình thang BDFP.
\(\Rightarrow KO=\dfrac{1}{2}\left(PF+BD\right)=\dfrac{1}{2}BP\)
Xét △BOP có: OK là trung tuyến và \(OK=\dfrac{1}{2}BP\)
\(\Rightarrow\)△BOP vuông tại O.
NV
18 tháng 3 2023
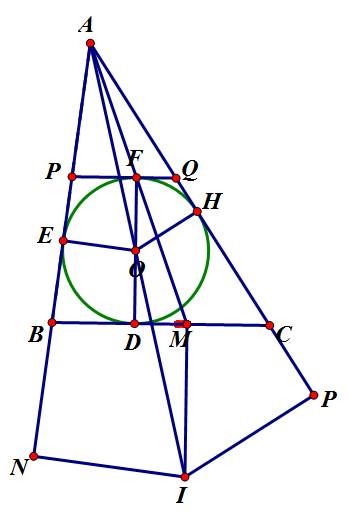
c) (O) tiếp xúc với AC tại H.
△ABC có (O) tiếp xúc với BC,AB,CA lần lượt tại D,E,H.
\(\Rightarrow BD=BE;AE=AH;CD=CH\)
\(BD+BE=AB-AE+BC-CD=AB+BC-AH-CH=AB+BC-AC\)
\(\Rightarrow BD=\dfrac{AB+BC-CA}{2}\left(3\right)\)
*Qua M kẻ đường thẳng vuông góc với BC cắt tia AO tại I.
*Hạ IN⊥AB tại N, IP⊥CA tại P.
Xét △AIM có: OF//IM \(\Rightarrow\dfrac{OF}{IM}=\dfrac{AO}{AI}\) (4) (hệ quả định lí Thales)
Xét △AIN có: OE//IN \(\Rightarrow\dfrac{OE}{IN}=\dfrac{AO}{AI}\) (5) (hệ quả định lí Thales)
Ta cũng có \(OE=OF\left(6\right)\) (bằng bán kính của (O) )
\(\left(4\right),\left(5\right),\left(6\right)\Rightarrow IM=IN\)
Dễ dàng chứng minh △BNI=△BMI (ch-cgv) nên \(\widehat{NBI}=\widehat{MBI}\)
\(\Rightarrow BI\) là phân giác của góc NBC hay BI là phân giác ngoài của △ABC.
Xét △ABC có: Phân giác trong góc A (AO) cắt phân giác ngoài góc B (BI) tại I.
\(\Rightarrow\)I là tâm đường tròn bàng tiếp ở đỉnh A.
Lại có IN⊥AB tại N, IM⊥BC tại M, IP⊥AC tại P.
\(\Rightarrow\)IN,IP,IM là các bán kính của (I).
\(\Rightarrow\)(I) tiếp xúc với AB,BC,CA lần lượt tại N,M,P.
\(\Rightarrow AN=AP;BN=BM;CM=CP\)
\(CM+CP=BC-BM+AP-AC=BC-AC+AN-BN=BC-AC+AB\)
\(\Rightarrow CM=\dfrac{BC+AB-AC}{2}\left(7\right)\)
\(\left(3\right),\left(7\right)\Rightarrow BD=CM\)
DV
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
Câu 4 đề 1:
Biến đổi miền D: \(x^2+y^2\le2x\Leftrightarrow x^2-2x+1+y^2\le1\)
\(\Leftrightarrow\left(x-1\right)^2+y^2\le1\)
Đặt \(\left\{{}\begin{matrix}x-1=r.cos\varphi\\y=r.sin\varphi\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1+r.cos\varphi\\y=r.sin\varphi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}0\le r\le1\\0\le\varphi\le2\pi\end{matrix}\right.\)
\(I=\int\limits^{2\pi}_0d\varphi\int\limits^1_0\left(2+r.cos\varphi\right).rdr=\int\limits^{2\pi}_0d\varphi\int\limits^1_0\left(2r+r^2.cos\varphi\right)dr\)
\(=\int\limits^{2\pi}_0d\varphi.\left(r^2+\dfrac{r^3}{3}cos\varphi\right)|^1_0=\int\limits^{2\pi}_0\left(1+\dfrac{1}{3}cos\varphi\right)d\varphi=2\pi\)
Câu 4 đề 2: sao câu này người ta ko cho biết chiều tính tích phân nhỉ? Coi như tính theo chiều dương đi.
\(\left\{{}\begin{matrix}P=x^2+xy\\Q=x+2xy\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}P'_y=x\\Q'_x=2y+1\end{matrix}\right.\)
Miền lấy tích phân là miền kín, áp dụng định lý Green:
\(I=\int\limits\int\limits^{ }_D\left(Q'_x-P'_y\right)dxdy=\int\limits\int\limits^{ }_D\left(2y-x+1\right)dxdy\)
Pt AC có dạng \(x=1\) và pt \(BC\) có dạng \(x=3-y\)
Chiếu lên Oy \(\Rightarrow\left\{{}\begin{matrix}0\le y\le2\\1\le x\le3-y\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^2_0dy\int\limits^{3-y}_1\left(2y-x+1\right)dx\)
\(=\int\limits^2_0dy\left(\left(2y+1\right)x-\dfrac{x^2}{2}\right)|^{3-y}_1\)
\(=\int\limits^2_0\left(-\dfrac{5}{2}y^2+6y-2\right)dy=\dfrac{4}{3}\)
13 tháng 6 2023
3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM
KN
2
NA
19 tháng 5 2021
a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được
PN
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2021
3.
\(\overrightarrow{AB}=\left(4;2\right)=2\left(2;1\right)\)
Do đó đường thẳng AB nhận \(\left(-1;2\right)\) là 1 vtpt
4.
\(\overrightarrow{AB}=\left(-a;b\right)\)
\(\Rightarrow\) Đường thẳng AB nhận (b;a) là 1 vtpt
Bài 3 nhìn không rõ, cơ may là đọc được đề câu 4