Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

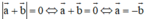
⇔ a→ và b→ là hai vec tơ đối nhau
⇔ a→ và b→ cùng phương, ngược hướng và có cùng độ dài.

\(\left| {\overrightarrow a + \overrightarrow b } \right| = 0 \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a = - \overrightarrow b \)
\(\overrightarrow a = - \overrightarrow b \) suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là hai vecto đối nhau nên chúng cùng phương, ngược hướng và có độ dài bằng nhau.

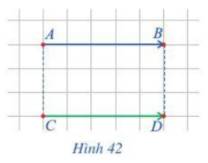
a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.

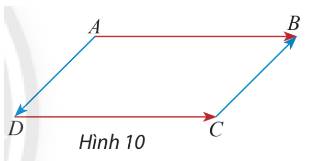
a) Ta có: \(AB = CD \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
\(AB//CD\) và \(\overrightarrow {AB} \), \(\overrightarrow {DC} \) có hướng từ trái sang phải
Suy ra \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
b) Ta có: \(AD = CB \Rightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\)
\(AD//CB\) và \(\overrightarrow {AD} \)có hướng từ trên xuống dưới, \(\overrightarrow {CB} \) có hướng từ dưới lên trên. Suy ra \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \) ngược hướng

Ta có: a→ + a→ = 2a→
Độ dài của vecto a→ + a→ bằng 2 lần độ dài của vecto a→
Hướng của vecto a→ + a→ cùng hướng với vecto a→

\(\)vectơ \(\overrightarrow c = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \) có độ dài gấp \(\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}\) lần vectơ \(\overrightarrow b \) và cùng hướng với vectơ \(\overrightarrow b \)
+) Nếu hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)cùng hướng và ngược lại
+) \(\left| {\overrightarrow c } \right| = \left| {\frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b } \right| = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|\). Suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)có cùng độ dài

A B C M N
Do M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC nên MN//BC.
Do vậy hai véc tơ \(\overrightarrow{NM}\) và \(\overrightarrow{BC}\) cùng phương.
Từ = 0, ta có
= 0, ta có 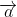 +
+ 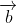 = 0 =>
= 0 => 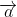 = –
= –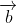
Điều này chứng tỏ hai vectơ có cùng độ dài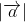 =
=  , cùng phương và ngược hướng
, cùng phương và ngược hướng