giải phương trình : x3+3x2-x-4=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
28 tháng 2 2021
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
28 tháng 2 2021
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
CM
7 tháng 9 2019
x3 + 3x2 – 2x – 6 = 0
⇔ (x3 + 3x2) – (2x + 6) = 0
⇔ x2(x + 3) – 2(x + 3) = 0
⇔ (x2 – 2)(x + 3) = 0
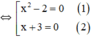
+ Giải (1): x2 – 2 = 0 ⇔ x2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
CM
26 tháng 11 2018
x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
CM
31 tháng 3 2018
x 3 + 3 x 2 + 2 x = 0 ⇔ x ( x 2 + 3 x + 2 ) = 0
⇔ x = 0 hoặc x 2 + 3 x + 2 = 0 ( 1 )
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
CM
12 tháng 9 2018
x3 – 3x2 + 3x - 1 = 0
⇔ (x – 1)3 = 0 (Hằng đẳng thức)
⇔ x – 1 = 0
⇔ x = 1.
Vậy tập nghiệm của phương trình là S={1}.
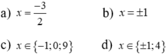
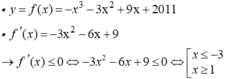
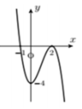
\(x^3+3x^2-x-4=0\left(1\right)\)
đặt \(y=x+\frac{3}{3}=x+1< =>x=y-1\)
thay vào pt: \(\left(y-1\right)^3+3\left(y-1\right)^2-\left(y-1\right)-4=0\)
\(y^3-3y^2+3y-1+3\left(y^2-2y+1\right)-y+1-4=0\)
\(y^3-3y^2+3y-1+3y^2-6y+3-y+1-4=0\)
\(y^3-4y-1=0\left(2\right)\)
ta tìm nghiệm của (2) dưới dạng \(y=u+v\)sao cho \(uv=\frac{4}{3}\)
thay \(y=u+v\)ta đc
\(\left(u+v\right)^3-4\left(u+v\right)-1=0\)
\(u^3+v^3+3uv\left(u+v\right)-4\left(u+v\right)-1=0\)
\(u^3+v^3+\left(u+v\right)\left(3uy-4\right)-1=0\)
\(u^3+v^3+\left(u+v\right).0-1=0\)
\(u^3+v^3-1=0\)
\(\hept{\begin{cases}u^3+v^3=1\\u^3v^3=\frac{4}{3}^3:27\end{cases}\hept{\begin{cases}u^3+v^3=1\\u^3v^3=\frac{64}{729}\end{cases}}}\)
\(< =>x^2-x+\frac{64}{729}=0\)
\(x^2-x=-\frac{64}{729}\)
\(x\left(x-1\right)=-\frac{64}{729}\)
\(\orbr{\begin{cases}x=-\frac{64}{729}\\x=-\frac{64}{129}+1=\frac{665}{729}\end{cases}}\)
\(KGTQ:u^3=-\frac{64}{729};v^3=\frac{665}{729}\)
bạn xét \(\xi\)thì ra đc nghiệm \(x_3\)
mình ko chắc có đúng ko nữa
sai đề r bạn