Cho tam giac ABC nội tiếp (O). Kẻ 2 đường cao BE&CF. CMR : OA vuông góc với EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
P
20 tháng 2 2017
Vẽ đường kính AK của đường tròn (O).
Chứng minh tứ giác BHCK là hình bình hành.
Gọi M là giao điểm của BC và HK suy ra M là trung điểm của BC nên OM là đường trung bình của tam giác AHK nên OM vuông góc với BC và AH = 2.OM
AH.BC=2.OM.BC = 4SBOC. Tương tự BH.AC=4SAOC, CH.AB=4SAOB
Cộng 3 đẳng thức được đpcm
20 tháng 4 2023
a: góc AEB=góc AHB=90 độ
=>ABHE nội tiếp
b: góc HED=góc ABC=1/2*sđ cung AC=góc ADC
=>HE//CD
12 tháng 11 2023
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
=>AEDB là tứ giác nội tiếp đường tròn đường kính AB
=>A,E,D,B cùng thuộc đường tròn đường kính AB
Tâm I của đường tròn này là trung điểm của AB
10 tháng 7 2023
a: Sửa đề: BFEC
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: góc ABK=1/2*sđ cung AK=90 độ
góc BAK=góc BAD+góc DAK
góc DAC=góc DAK+góc CAK
mà góc BAD=góc CAK
nên góc BAK=góc DAC
Xét ΔABK vuông tại B và ΔADC vuông tại D có
góc BAK=góc DAC
=>ΔABK đồng dạng với ΔADC
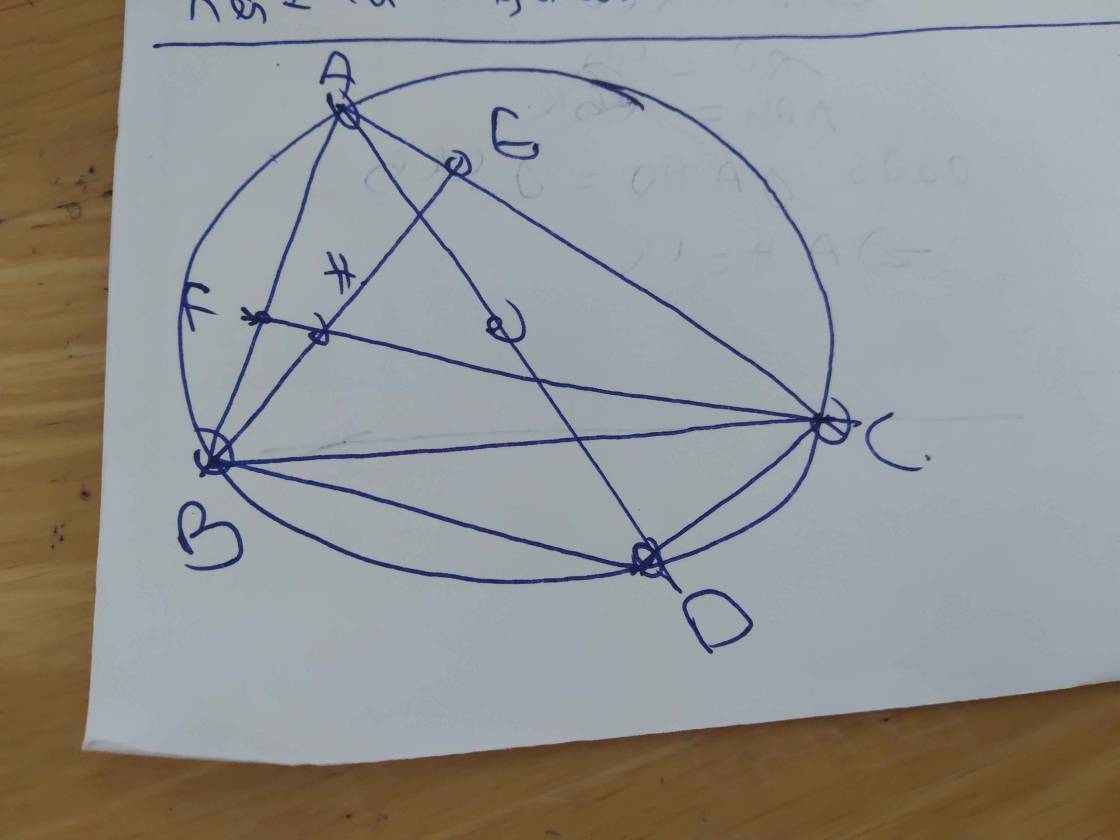
Hình vẽ:
Lời giải:
Kẻ $Ax$ là tiếp tuyến của $(O)$
Khi đó: $Ax\perp OA(1)$
Mặt khác:
Dễ thấy tứ giác $BFEC$ có $\widehat{BFC}=\widehat{BEC}=90^0$ và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp.
$\Rightarrow \widehat{AFE}=\widehat{ACB}$
Mà: $\widehat{ACB}=\widehat{xAB}$ (tính chất góc tạo bởi tiếp tuyến và dây cung thì bằng góc nt chắn cung đó)
Suy ra $\widehat{AFE}=\widehat{xAB}$. Mà 2 góc này ở vị trí so le trong nên $Ax\parallel EF(2)$
Từ $(1);(2)\Rightarrow OA\perp EF$ (đpcm)