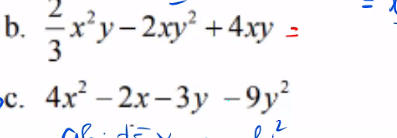phân tích các đt trên thành nhân tử ::>>>
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VN
1
Những câu hỏi liên quan
HN
4
LM
2
XO
26 tháng 12 2020
a) 10x + 15y = 5(2x + 3y)
b) x2 - 2xy - 4 + y2
= (x2 - 2xy + y2) - 4
= (x - y)2 - 22
= (x - y + 2)(x - y - 2)
c) x(x + y) - 3x - 3y
= x(x + y) -3(x + y)
= (x - 3)(x + y)
26 tháng 12 2020
a, \(10x+15y=5\left(2x+3y\right)\)
b, \(x^2-2xy-4+y^2=\left(x-y\right)^2-4=\left(x-y-2\right)\left(x-y+2\right)\)
c, \(x\left(x+y\right)-3x-3y=x\left(x+y\right)-3\left(x+y\right)=\left(x-3\right)\left(x+y\right)\)
BQ
0
8 tháng 8 2016
\(x-4\)
\(\left(\sqrt{2}\right)^2-4\)
\(=\left(\sqrt{2}-2\right)\left(\sqrt{2}+2\right)\)
NT
2
NH
20 tháng 9 2020
\(=\left(\sqrt{2x}\right)^2-\left(\sqrt{y}\right)^2\)
\(=\left(\sqrt{2x}-\sqrt{y}\right)\left(\sqrt{2x}+\sqrt{y}\right)\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 9 2024
3\(x\) - y
= (\(\sqrt{3x}\))2 - (\(\sqrt{y}\))2
= (\(\sqrt{3x}\) - \(\sqrt{y}\)).(\(\sqrt{3x}\) + \(\sqrt{y}\))
NT
2
20 tháng 9 2020
x - 3 = ( √x )2 - ( √3 )2 = ( √x - √3 )( √x + √3 ) < với x > 0 >
9 tháng 6 2016
b, \(a+b+2\sqrt{a.b}=\sqrt{a^2}+\sqrt{b^2}+2\sqrt{ab}=\left(\sqrt{a}+\sqrt{b}\right)^2\) ( Vì a, b >= 0 )
c, \(a+b-2\sqrt{a.b}=\sqrt{a^2}+\sqrt{b^2}-2\sqrt{ab}=\left(\sqrt{a}-\sqrt{b}\right)^2\)( Vì a, b >= 0 )
TQ
2
17 tháng 6 2016
1) \(3x^2+5x-8=3x^2-3x+8x-8\)
\(=3x\left(x-1\right)+8\left(x-1\right)\)
\(=\left(x-1\right)\left(3x+8\right)\)
2) \(2x^2-x-3=2x^2+2x-3x-3\)
\(=2x\left(x+1\right)-3\left(x+1\right)\)
\(=\left(x+1\right)\left(2x-3\right)\)
TN
17 tháng 6 2016
1)3x2+5x-8
=3x2+8x-3x-8
=x(3x+8)-1(3x+8)
=(x-1)(3x+8)
2)2x2-x-3
=2x2-3x+2x-3
=x(2x-3)+1(2x-3)
=(x+1)(2x-3)
Chúc bạn học tốt :) (tên bạn ấn tượng thật đó )
H
1
14 tháng 8 2020
\(x-7=\left(\sqrt{x}\right)^2-\left(\sqrt{7}\right)^2=\left(\sqrt{x}-\sqrt{7}\right)\left(\sqrt{x}+\sqrt{7}\right)\)( \(x\ge0\))
\(x-6\sqrt{x}+9=\left(\sqrt{x}\right)^2-2.3.\sqrt{x}+3^2=\left(\sqrt{x}-3\right)^2\)( \(x\ge0\))
Em mới lớp 8 nên không dám chắc ạ :(
b) \(\dfrac{2}{3}x^2y-2xy^2+4xy=2xy\left(\dfrac{1}{3}x-y+2\right)\)
c) \(4x^2-2x-3y-9y^2\)
\(=\left(2x-3y\right)\left(2x+3y\right)-\left(2x+3y\right)\)
\(=\left(2x+3y\right)\left(2x-3y-1\right)\)