hãy biểu diễn các điểm A(-2; 2), B(3; 3), C(2; -2) trên mặt phẳng tọa độ Oxy. Sau đó tính diện tích tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TA
6


HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Dễ thấy:
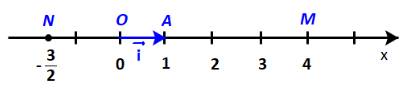
vectơ \(\overrightarrow {OM} \) cùng hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {OM} } \right| = 4 = 4\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {OM} = 4\,.\,\overrightarrow i \)
Tương tự, vectơ \(\overrightarrow {ON} \) ngược hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {ON} } \right| = \frac{3}{2} = \frac{3}{2}\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {ON} = - \frac{3}{2}\,.\,\overrightarrow i \)

CM
1 tháng 4 2017
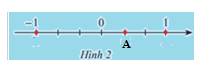
a) Vẽ trục và biểu diễn các điểm

b) Ta có:
A có tọa độ là –1, B có tọa độ là 2 nên 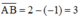
M có tọa độ là 3, N có tọa độ là –2 nên 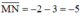


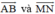 . Từ đó suy ra hai vec tơ
. Từ đó suy ra hai vec tơ 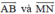 ngược hướng.
ngược hướng.
Đường thẳng AB →qua A(-2; 2) \(\overrightarrow{AB}\) = (5; 1) → VTPT \(\overrightarrow{n}\) = (1; -5)
→ AB: (x+2) -5(y-2) = 0
→ AB: x - 5y + 12 = 0
d(C/AB) = \(\frac{\left|2+5.2+12\right|}{\sqrt{1^2+5^2}}\) = \(\frac{24}{\sqrt{26}}\)
AB = \(\sqrt{\left(3+2\right)^2+\left(3-2\right)^2}=\sqrt{26}\)
\(\Rightarrow S_{ABC}=\frac{1}{2}.AB.d\left(C,AB\right)=\frac{1}{2}.\frac{24}{\sqrt{26}}.\sqrt{26}=12\)
cái ni mà hình lp 10 hả mék ???