Chứng minh rằng từ đẳng thức ad=bc (c, d\(\ne\)0), ta có thể suy ra được tỉ lệ thức a/c=b/d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ad=bc=>ad:dc=bc:dc=>\frac{ad}{dc}=\frac{bc}{dc}=>\frac{a}{c}=\frac{b}{d}\)
\(ad=bc\Rightarrow\frac{ad}{cd}=\frac{bc}{cd}\Rightarrow\frac{a}{c}=\frac{b}{d}\)

Ta có :
\(ad=bc\left(1\right)\)
Chia cả 2 vế của \(\left(1\right)\) cho \(bd\) ta được :
\(VT=\dfrac{ad}{bd}=\dfrac{a}{b}\left(2\right)\)
\(VP=\dfrac{bc}{bd}=\dfrac{c}{d}\left(3\right)\)
Từ \(\left(2\right)+\left(3\right)\Leftrightarrowđpcm\)
Từ có đẳng thức: \(ad=bc\)
\(\Rightarrow\dfrac{ad}{cd}=\dfrac{bc}{cd}\) \(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\) (đpcm)

Ta có: ad=bc (1)
Chia 2 vế của (1) cho bd ta có:
\(VT=\frac{ad}{bd}=\frac{a}{b}\left(2\right)\)
\(VP=\frac{bc}{bd}=\frac{c}{d}\left(2\right)\)
Từ (1) và (2) ta có: \(\frac{a}{b}=\frac{c}{d}\)

Ta có: ad = bc; c ≠ 0; d ≠ 0 suy ra cd ≠ 0
Chia cả 2 vế cho cd. Suy ra:
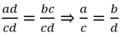

\(ad=bc\Rightarrow ad:dc=bc:dc\Rightarrow\frac{ad}{dc}=\frac{bc}{dc}\Rightarrow\frac{a}{c}=\frac{b}{d}\)

Trần Trương Quỳnh Hoa và câu hỏi tương tự có đấy, tick cho mình nha!
\(ad=bc=>ad:dc=bc:dc=>\frac{ad}{dc}=\frac{bc}{dc}=>\frac{a}{c}=\frac{b}{d}\)
nếu a/c=b/d thì a.d/cd=bc/cd=>ad=bcthí a/c=b/d