CMR : nếu 2 đường thẳng Song song thì 2 tia pg của cặp góc trong cùng phía vuông góc với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì hai đường song song thì có hai góc cùng phía bù nhau
=> Tổng hai góc cùng phía = 1800
=> Tổng hai góc phân giác của hai góc cùng phía = 900
=> Hai tia phân giác của hai góc trong cùng phía là góc vuông (ĐPCM)

A B O a b 1 2 1 2 C D
Cho hình vẽ như trên.
Ta có:
a//b => góc CAB + góc ABD = 1800 (trong cùng phía)
Mà Â1= Â2, góc B1 góc B2
Nên 2.Â2 + 2. góc B2 = 1800
=> Â2 + góc B1 = 900
Tam giác AOB có:
Â2 + góc B1 + AÔB =1800
Hay AÔb = 1800 - (Â2 + góc B1) = 1800 - 900 = 900
=>OA vuông góc với OB (ĐPCM)

A B C D E O a b c 1 2 1 2
ta có: a//b => \(\widehat{A}+\widehat{B}=180^o\)
\(\widehat{A}_1+\widehat{B}_1=\frac{\widehat{A}}{2}+\frac{\widehat{B}}{2}=\frac{\widehat{A}+\widehat{B}}{2}=\frac{180^o}{2}=90^o\)
\(\widehat{O}=180^o-\left(\widehat{A_1}+\widehat{B_1}\right)=180^o-90^o=90^o\)
=> AO_|_BO tại O

Giải

Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F
Ta có: (widehat {BEF} + widehat {EFD} = 180^circ ) (hai góc trong cùng phía)
(eqalign{
& widehat {{E_1}} = {1 over 2}widehat {{ m{BEF}}}left( {gt} ight) cr
& widehat {{F_1}} = {1 over 2}widehat {EFD}left( {gt} ight) cr} )
( Rightarrow widehat {{E_1}} + widehat {{F_1}} = {1 over 2}left( {widehat {{ m{BEF}}} + widehat {EFD}} ight) = 90^circ )
Trong ∆EKF, ta có:
(widehat {EKF} = 180^circ – left( {widehat {{E_1} + widehat {{F_1}}}} ight) = 180^circ – 90^circ = 90^circ )
Vậy (EK ot FK).
Hai đường thẳng song song nhau và có một đường thẳng cắt hai đường thẳng đó sẽ tạo ra ít nhất 1 cặp góc so le trong bằng nhau.
Ta có: Hai tia phân giác của 2 góc so le trong đó.
=> Hai góc tạo thành bởi hai tia phân giác bằng nhau.
=> Hai góc đó là hai góc đồng vị bằng nhau.
=> ĐPCM

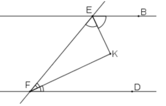
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F
Ta có: ∠BEF + ∠EFD = 180o (hai góc trong cùng phía)
+) Do EK là tia phân giác của góc ∠ BEF nên:
∠E1 = 1/2 .∠ (BEF) (1)
+) Do FK là tia phân giác của góc EFD nên :
∠F1 = 1/2 .∠EFD (2)
Từ (1) và (2) suy ra:
∠E1 +∠F1 =1/2 .(∠BEF + ∠EFD ) = 1/2 . 180º = 90º ( ∠BEF + ∠EFD = 180º hai góc trong cùng phía)
Trong ΔEKF,ta có:
∠EKF = 180o-(∠E1 + ∠F1) = 180o-90o=90o
Vậy EK ⊥FK

O A B x y x' y'
góc AOy + góc OAy' = 180 độ (xy//x'y') (1)
góc AOB = góc AOy : 2 (OB là tia phân giác của góc AOy) (2)
góc OAB = góc OAy' : 2 (AB là tia phân giác của góc OAy') (3)
Từ (1); (2); (3) => góc AOB + góc OAB = (góc AOy + góc OAy') : 2 = 180 độ : 2 = 90 độ
=> tam giác OAB vuông tại B (DHNB)
=> OB vuông góc với AB (t/c)
a b A B C 1 2 1 2 c
a // b
c x a = A
c x b = B
\(\begin{cases}\widehat{A_1}=\widehat{A_2}=\frac{1}{2}.\widehat{A}\\\widehat{B_1}=\widehat{B_2}=\frac{1}{2}.\widehat{B}\end{cases}\)
Mặt khác
\(\widehat{A}+\widehat{B}=180^0\)
=> \(\widehat{A_1}+\widehat{B_1}=\frac{\widehat{A}}{2}+\frac{\widehat{B}}{2}\)
=> \(\widehat{A_1}+\widehat{B_1}=\frac{\widehat{A}+\widehat{B}}{2}\)
=> \(\widehat{A_1}+\widehat{B_1}=\frac{180^0}{2}=90^0\)
Xét \(\Delta ABC\) có :
\(\widehat{A_1}+\widehat{B_1}+\widehat{C}=180^0\)
=> \(90^0+\widehat{C}=180^0\)
=> \(\widehat{C}=90^0\) ( đpcm )
Ta có:
a//b => góc CAB + góc ABD = 1800 (trong cùng phía)
Mà Â1= Â2, góc B1 góc B2
Nên 2.Â2 + 2. góc B2 = 1800
=> Â2 + góc B1 = 900
Tam giác AOB có:
Â2 + góc B1 + AÔB =1800
Hay AÔb = 1800 - (Â2 + góc B1) = 1800 - 900 = 900
=>OA vuông góc với OB (ĐPCM)