TÌM x
a, \(\sqrt{x+2\sqrt{x}+1}\)=3
b,\(\sqrt{2x-1}+1\)=2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
25 tháng 9 2023
a) \(\sqrt{x-1}+\sqrt{x+3}+2\sqrt{\left(x+3\right)\left(x-1\right)}=-\left(x+3+x-1-6\right)\)\(\left(Đk:x\ge1\right)\)
\(\left(\sqrt{x-1}+\sqrt{x+3}\right)^2+\sqrt{x-1}+\sqrt{x-3}-6=0\)
\(\left(\sqrt{x-1}+\sqrt{x+3}+3\right)\left(\sqrt{x-1}+\sqrt{x+3}-2\right)=0\)
Đến đây em xét các trường hợp rồi bình phương lên là được nha
b) \(\sqrt{3x-2}+\sqrt{x-1}=3x-2+x-1-6+2\sqrt{\left(3x-2\right)\left(x-1\right)}\left(Đk:x\ge1\right)\)
\(\left(\sqrt{3x-2}+\sqrt{x-1}\right)^2-\left(\sqrt{3x-2}+\sqrt{x-1}\right)-6=0\)
\(\left(\sqrt{3x-2}+\sqrt{x-1}-3\right)\left(\sqrt{3x-2}+\sqrt{x-1}+2\right)=0\)
Đến đây em xét các trường hợp rồi bình phương lên là được nha
AH
Akai Haruma
Giáo viên
25 tháng 9 2023
a/ ĐKXĐ: $x\geq 1$
Đặt $\sqrt{x-1}=a; \sqrt{x+3}=b$ thì pt trở thành:
$a+b+2ab=6-(a^2+b^2)$
$\Leftrightarrow a^2+b^2+2ab+a+b-6=0$
$\Leftrightarrow (a+b)^2+(a+b)-6=0$
$\Leftrightarrow (a+b-2)(a+b+3)=0$
Hiển nhiên do $a\geq 0; b\geq 0$ nên $a+b+3>0$. Do đó $a+b-2=0$
$\Leftrightarrow a+b=2$
Mà $b^2-a^2=(x+3)-(x-1)=4$
$\Leftrightarrow (b-a)(b+a)=4\Leftrightarrow (b-a).2=4\Leftrightarrow b-a=2$
$\Rightarrow \sqrt{x+3}=b=(a+b+b-a):2=(2+2):2=2$
$\Leftrightarrow x=1$ (tm)
Q
1
14 tháng 7 2023
a: =>2x^2-3x-2=6x+2
=>2x^2-9x-4=0
=>\(x=\dfrac{9\pm\sqrt{113}}{4}\)
b: \(=\dfrac{x-3\sqrt{x}+4-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
TD
a) \(\dfrac{2x^2-3x-2}{2x+1}\)=3
b)B=\(\dfrac{x-3\sqrt{x}+4}{x-2\sqrt{x}}\)=\(\dfrac{1}{\sqrt{x}-2}\)
1
14 tháng 7 2023
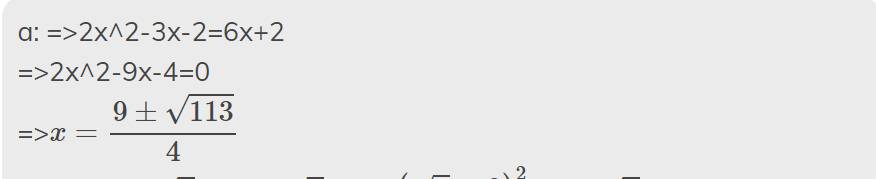
b: =>x-3căn x+4=căn x
=>(căn x-2)^2=0
=>căn x-2=0
=>x=4(loại)
VP
3
28 tháng 8 2021
a: Ta có: \(x-3\sqrt{x+1}=-3\)
\(\Leftrightarrow\sqrt{9x+9}=x+3\)
\(\Leftrightarrow x^2+6x+9-9x-9=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
HP
28 tháng 8 2021
a, ĐK: \(x\ge-1\)
\(x-3\sqrt{x+1}=-3\)
\(\Leftrightarrow x+3\left(1-\sqrt{x+1}\right)=0\)
\(\Leftrightarrow x-\dfrac{3x}{1+\sqrt{x+1}}=0\)
\(\Leftrightarrow x\left(1-\dfrac{3}{1+\sqrt{x+1}}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\1+\sqrt{x+1}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
MH
27 tháng 9 2023
a) \(\sqrt{2x}=12\left(đk:x\ge0\right)\)
\(2x=144\)
\(x=72\)
b) \(\sqrt{9x^2-6x}+1=10\)\(\left(Đk:x\le0;x\ge\dfrac{2}{3}\right)\)
\(\sqrt{9x^2-6x}=9\)
\(9x^2-6x=81\)
\(\left(3x-1\right)^2=82\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{82}+1}{3}\\x=\dfrac{1-\sqrt{82}}{3}\end{matrix}\right.\)
c) \(x^2\sqrt{5}-\sqrt{125}=0\)
\(x^2\sqrt{5}=5\sqrt{5}\)
\(x^2=5\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{5}\\x=-\sqrt{5}\end{matrix}\right.\)
28 tháng 8 2023
\(a)ĐK:x\ge-1\\ \Leftrightarrow x+1=2\sqrt{x+1}\\ \Leftrightarrow x^2+2x+1=4x+4\\ \Leftrightarrow x^2+2x-4x+1-4=0\\ \Leftrightarrow x^2-2x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{3;-1\right\}\)
\(b)ĐK:x\ge2\\ \Leftrightarrow2x-4=\sqrt{x-2}\\ \Leftrightarrow4x^2-16x+16=x-2\\ \Leftrightarrow4x^2-16x-x+16+2=0\\ \Leftrightarrow4x^2-17x+18=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{4}\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{9}{4};2\right\}\)
\(c)ĐK:x\ge3\\ \Leftrightarrow2\sqrt{9\left(x-3\right)}-\dfrac{1}{5}\sqrt{25\left(x-3\right)}-\dfrac{1}{7}\sqrt{49\left(x-3\right)}=20\\ \Leftrightarrow2.3\sqrt{x-3}-\dfrac{1}{5}\cdot5\sqrt{x-3}-\dfrac{1}{7}\cdot7\sqrt{x-3}=20\\ \Leftrightarrow6\sqrt{x-3}-\sqrt{x-3}-\sqrt{x-3}=20\\ \Leftrightarrow4\sqrt{x-3}=20\\ \Leftrightarrow\sqrt{x-3}=5\\ \Leftrightarrow x-3=25\\ \Leftrightarrow x=25+3\\ \Leftrightarrow x=28\left(tm\right)\)
Vậy \(S=\left\{28\right\}\)
24 tháng 12 2023
a: \(\left(2x-3\right)^2=\left|3-2x\right|\)
=>\(\left\{{}\begin{matrix}\left|2x-3\right|>=0\\\left(2x-3\right)^2=\left(2x-3\right)\end{matrix}\right.\Leftrightarrow\left(2x-3\right)^2-\left(2x-3\right)=0\)
=>\(\left(2x-3\right)\left(2x-3-1\right)=0\)
=>\(\left(2x-3\right)\left(2x-4\right)=0\)
=>\(\left[{}\begin{matrix}2x-3=0\\2x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\end{matrix}\right.\)
b: \(\left(x-1\right)^2+\left(2x-1\right)^2=0\)
=>\(x^2-2x+1+4x^2-4x+1=0\)
=>\(5x^2-6x+2=0\)
\(\Delta=\left(-6\right)^2-4\cdot5\cdot2=36-20\cdot2=-4< 0\)
=>Phương trình vô nghiệm
c: ĐKXĐ: x>=0
\(x-2\sqrt{x}=0\)
=>\(\sqrt{x}\cdot\sqrt{x}-2\cdot\sqrt{x}=0\)
=>\(\sqrt{x}\left(\sqrt{x}-2\right)=0\)
=>\(\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
d: \(\left(x-1\right)^2+\dfrac{1}{7}=0\)
mà \(\left(x-1\right)^2+\dfrac{1}{7}>=\dfrac{1}{7}>0\forall x\)
nên \(x\in\varnothing\)
25 tháng 8 2021
a)√x−1=2(x≥1)
\(x-1=4
\)
x=5
b)
\(\sqrt{3-x}=4\) (x≤3)
\(\left(\sqrt{3-x}\right)^2=4^2\)
x-3=16
x=19
26 tháng 8 2021
a: Ta có: \(\sqrt{x-1}=2\)
\(\Leftrightarrow x-1=4\)
hay x=5
b: Ta có: \(\sqrt{3-x}=4\)
\(\Leftrightarrow3-x=16\)
hay x=-13
c: Ta có: \(2\cdot\sqrt{3-2x}=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{3-2x}=\dfrac{1}{4}\)
\(\Leftrightarrow-2x+3=\dfrac{1}{16}\)
\(\Leftrightarrow-2x=-\dfrac{47}{16}\)
hay \(x=\dfrac{47}{32}\)
d: Ta có: \(4-\sqrt{x-1}=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{7}{2}\)
\(\Leftrightarrow x-1=\dfrac{49}{4}\)
hay \(x=\dfrac{53}{4}\)
e: Ta có: \(\sqrt{x-1}-3=1\)
\(\Leftrightarrow\sqrt{x-1}=4\)
\(\Leftrightarrow x-1=16\)
hay x=17
f:Ta có: \(\dfrac{1}{2}-2\cdot\sqrt{x+2}=\dfrac{1}{4}\)
\(\Leftrightarrow2\cdot\sqrt{x+2}=\dfrac{1}{4}\)
\(\Leftrightarrow\sqrt{x+2}=\dfrac{1}{8}\)
\(\Leftrightarrow x+2=\dfrac{1}{64}\)
hay \(x=-\dfrac{127}{64}\)
HP
27 tháng 8 2021
a, \(x+1\ge0\Leftrightarrow x\ge-1\)
b, \(1-2x\ge0\Leftrightarrow x\le\dfrac{1}{2}\)
c, \(\left\{{}\begin{matrix}x+1\ge0\\x-2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ge2\end{matrix}\right.\Leftrightarrow x\ge2\)
HP
27 tháng 8 2021
d, \(\left\{{}\begin{matrix}2-3x\ge0\\1-2x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{2}{3}\\x\le\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow x\le\dfrac{1}{2}\)
e, \(\left\{{}\begin{matrix}\sqrt{3}-2x\ge0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{\sqrt{3}}{2}\\x\ne1\end{matrix}\right.\Leftrightarrow x\le\dfrac{\sqrt{3}}{2}\)
câu b nhầm nhé
b/ \(\Rightarrow\sqrt{2x-1}=2x-1\Rightarrow2x-1=\left(2x-1\right)^2\)
\(\Rightarrow\left(2x-1\right)\left(1-2x+1\right)=0\)
\(\Rightarrow2x-1=0\Rightarrow2x=1\Rightarrow x=\frac{1}{2}\)
hoặc \(2-2x=0\Rightarrow2x=2\Rightarrow x=1\)
vậy x = 1/2 ; x = 1