giải pt nghiệm nguyên
x3-y3=2xy+13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DT
1
Những câu hỏi liên quan
15 tháng 6 2022
\(pt< =>\left(x-y\right)^2+xy=\left(x-y\right)\left(xy+2\right)+9\)
\(< =>\left(y-x\right)\left(xy+2+y-x\right)+xy+2+y-x-\left(y-x\right)=11\)
\(< =>\left(y-x+1\right)\left(xy+2+y-x\right)-\left(y-x+1\right)=10\)
\(< =>\left(x-y+1\right)\left(x-y-1-xy\right)=10\)
đến đây giải hơi bị khổ =))
DV
2
XO
1 tháng 1 2022
x3 + y3 + 1 = 6xy
<=> (x + y)3 - 3xy(x + y) + 1 = 6xy
<=> (x + y)3 + 8 - 3xy(x + y + 2) = 7
<=> (x + y + 2)(x2 - xy + y2 + 2x + 2y + 4) = 7
Đến đây bạn tự giải tiếp
DV
0
XO
17 tháng 4 2022
x3 - 6xy + y3 = 8
<=> (x + y)3 - 3xy(x + y) - 6xy + 8 = 16
<=> (x + y + 2)(x2 + y2 - xy - 2x - 2y + 4) = 16
<=> \(\left(x+y+2\right)\left[\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\right]=16\)
Nhận thấy \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\ge0\)
=> x + y + 2 > 0
Khi đó 16 = 1.16 = 2.8 = 4.4
Lập bảng
| x + y + 2 | 1 | 16 | 4 | 2 | 8 | |
| \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\) | 16 | 1 | 4 | 8 | 2 | |
| x | ||||||
| y | | |
Đến đó bạn thế x qua y rồi làm tiếp nha
BD
1
TT
22 tháng 1 2021
Ta có: \(xy^2+2xy+x=32y \)
⇔ \(x\left(y^2+2y+1\right)=32y\)
⇔\(x=\dfrac{32y}{\left(y+1\right)^2}\)
⇔\(x=\dfrac{32y-32+32}{\left(y+1\right)^2}\)
⇔\(x=\dfrac{32\left(y+1\right)}{\left(y+1\right)^2}-\dfrac{32}{\left(y+1\right)^2}\)
⇔\(x=\dfrac{32}{y+1}-\dfrac{32}{\left(y+1\right)^2}\)
Để x là số dương ⇒ \(\left(y+1\right)^2\)∈ \(U_{\left(32\right)}\)={-32 ;-16;-8;-4;-2;-1;1;2;4;8;16;32}
Nhưng \(\left(y+1\right)^2\)là số chính phương ⇒ \(\left(y+1\right)^2\)∈ {1;4;16}
⇒\(\left[{}\begin{matrix}\left(y+1\right)^2=1\\\left(y+1\right)^2=4\\\left(y+1\right)^2=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y+1=1\\y+1=2\\y+1=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=0\\y=1\\y=3\end{matrix}\right.\)
Thay :
y = 0 ⇒ x = 0
y = 1 ⇒ x = 8
y = 3 ⇒ x = 6
Vậy x;y = ( 0;0) ; ( 8;1) ; ( 6;3)
M
1
19 tháng 10 2017
ta có: \(5x-3y=2xy-11\)
<=>\(2x-2xy+3-3y+3x=-8\)
<=>\(2x\left(1-y\right)+3\left(1-y\right)+\frac{3}{2}\left(2x+3\right)=-\frac{7}{2}\)
<=>\(\left(2x+3\right)\left(1-y\right)+\frac{3}{2}\left(2x+3\right)=-\frac{7}{2}\)
<=>\(\left(2x+3\right)\left(1-y+\frac{3}{2}\right)=-\frac{7}{2}\)
<=>\(\left(2x+3\right)\left(2-2y+3\right)=-7\)
TH1: \(\hept{\begin{cases}2x+3=1\\2-2y+3=-7\end{cases}\Rightarrow\hept{\begin{cases}x=-1\\y=6\end{cases}}}\)
TH2:\(\hept{\begin{cases}2x+3=-1\\2-2y+3=7\end{cases}\Rightarrow\hept{\begin{cases}x=-2\\y=-1\end{cases}}}\)
TH3:\(\hept{\begin{cases}2x+3=7\\2-2y+3=-1\end{cases}\Rightarrow\hept{\begin{cases}x=2\\y=3\end{cases}}}\)
TH4:\(\hept{\begin{cases}2x+3=-7\\2-2y+3=1\end{cases}\Rightarrow\hept{\begin{cases}x=-5\\y=2\end{cases}}}\)
Vậy nghiệm của pt là: (x;y)={ (-1;6);(-2;-1);(2;3);(-5;2)}
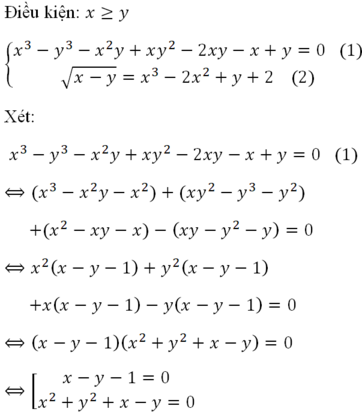
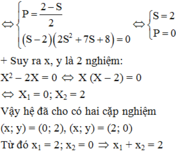
\(x^3-y^3=2xy+13\)
\(\Leftrightarrow\left(x-y\right)^3+3xy\left(x-y\right)=2xy+13\)
\(\Leftrightarrow a^3-13=b\left(2-3a\right)\)(\(a=x-y,b=xy\))
\(\Rightarrow a^3-13⋮\left(2-3a\right)\)
\(\Rightarrow27\left(a^3-13\right)⋮\left(3a-2\right)\)
\(\Leftrightarrow27a^3-8-343=\left(3a-2\right)\left(9a^2+6a+4\right)+343⋮\left(3a-2\right)\)
suy ra \(3a-2\inƯ\left(343\right)=Ư\left(7^3\right)\)
\(\Rightarrow a\in\left\{1,3,17,115\right\}\).
Suy ra các bộ \(\left(a,b\right)\)thỏa mãn là: \(\left(1,12\right),\left(3,-2\right),\left(17,-100\right),\left(115,-4434\right)\).
Với bộ \(\left(1,12\right)\)ta có:
\(\hept{\begin{cases}x-y=1\\xy=12\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=4,y=3\\x=-3,y=-4\end{cases}}\)
Tương tự với các bộ còn lại suy ra nghiệm của phương trình.