Giải bất phương trình (-3x+6).(x-5) < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
7 tháng 4 2019
a) \(x^2-5x+6< 0\)
\(\Leftrightarrow x^2-2x-3x+6< 0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)< 0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-2>0\\x-3< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>2\\x< 3\end{cases}}}\)
\(\Leftrightarrow2< x< 3\)
Vậy \(2< x< 3\)là các giá trị cần tìm của bất phương trình
b) \(\frac{2x\left(3x-5\right)}{x^2+1}< 0\)
\(\Leftrightarrow2x\left(3x-5\right)< 0\)(vì \(x^2+1>0\forall x\) )
\(\Leftrightarrow\hept{\begin{cases}2x>0\\3x-5< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\3x< 5\end{cases}\Leftrightarrow}\hept{\begin{cases}x>0\\x< \frac{5}{3}\end{cases}}}\)
\(\Leftrightarrow0< x< \frac{5}{3}\)
Vậy \(0< x< \frac{5}{3}\)là các giá trị cần tìm của bất phương trình
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
NT
1
15 tháng 4 2019
\(x^3-2x^2+3x-6< 0\)
\(\Leftrightarrow x^2\left(x-2\right)+3\left(x-2\right)< 0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+3\right)< 0\)
\(\Leftrightarrow x-2< 0\) (Vì \(x^2+3>0\) \(\forall x\))
\(\Leftrightarrow x< 2\)
V...
15 tháng 7 2023
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
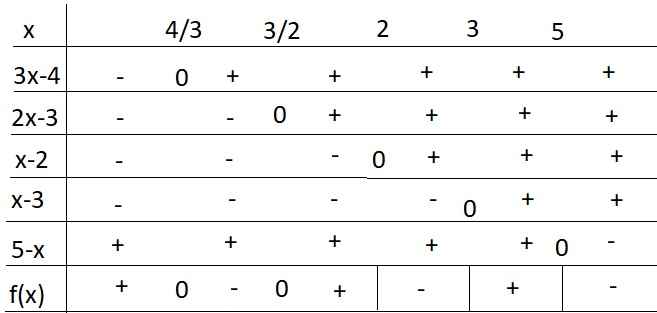
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
12 tháng 5 2023
1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
Trả lời:
\(\left(-3x+6\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}-3x+6< 0\\x-5>0\end{cases}}\) hoặc \(\hept{\begin{cases}-3x+6>0\\x-5< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>2\\x>5\end{cases}}\) hoặc \(\hept{\begin{cases}x< 2\\x< 5\end{cases}}\)
Vậy x > 5; x < 2 là nghiệm của pt.
\(\left(-3x+6\right)\left(x-5\right)< 0\)
\(\Leftrightarrow-3\left(x-2\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\left(x-2\right)\left(x-5\right)>0\)
\(\Leftrightarrow\hept{\begin{cases}x-2>0\\x-5>0\end{cases}}\)hoặc \(\hept{\begin{cases}x-2< 0\\x-5< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>2\\x>5\end{cases}}\)hoặc \(\hept{\begin{cases}x< 2\\x< 5\end{cases}}\)
hay \(\orbr{\begin{cases}x>5\\x< 2\end{cases}}\)
Vậy nghiệm của BPT là \(x>5\)hoặc \(x< 2\)