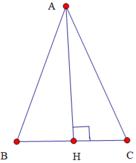
cho tam giác abc cân tại a.đường cao ah.biết BC=a,AH=h.Tính độ dài cạnh bên theo a,h
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
19 tháng 2 2021
B A C H Căn 32 9 ?
Áp dụng định lý Pytago ta có : BH2 + HC2 = BC2
Hay \(\sqrt{ }\)32 2 + 92= BC2
32 + 81 = BC2
113 = BC2
\(\sqrt{ }\)113 = BC
28 tháng 4 2016
Bạn tự vẽ hình nha!!!
AH là đường cao của tam giác ABC cân tại A
=> AH là đường trung trực của tam giác ABC.
=> H là trung điểm của BC
=> HB = HC = BC/2 = 6/2 = 3
Tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\) (định lí Pytago)
\(AH^2=AB^2-BH^2\)
\(AH^2=5^2-3^2\)
\(AH^2=25-9\)
\(AH^2=16\)
\(AH=\sqrt{16}\)
\(AH=4\)
9 tháng 1 2016
CÁc câu kia dễ mình không ns còn câu d trong 3 điểm thẳng hàng =180 độ
25 tháng 6 2020
tự kẻ hình nha
a) xét tam giác ABH và tam giác ACH có
AB=AC(gt)
ABC=ACB(gt)
AHB=AHC(=90 độ)
=> tam giác ABH= tam giác ACH( ch-gnh)
b) từ tam giác ABH= tam giác ACH=> HB=HC( hai cạnh tương ứng)
=>HB=HC=BC/2=12/2=6cm
ta có AH^2=AB^2-BH^2=10^2-6^2=100-36=64=8^2
=> AH=8 (AH>0)
d) vì HB=HC=> H là trung điểm của BC=> AH là trung tuyến
mà G là trọng tâm của tam giác ABC=> G thuộc AH=> A,G,H thẳng hàng
c) vì AH vừa là trung tuyến vừa là đường cao => AH là trung trực của BC
vì G thuộc AH=> GB=GC
xét tam giác ABG và tam giác ACG có
AB=AC(gt)
GB=GC( cmt)
AG chung
=> tam giác ABG= tam giác ACG(ccc)
chế cho phần d) lên trước phần c) cho đỡ phải chứng minh lại thôi chứ không có j đâu
10 tháng 9 2021
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH^2+16HB-225=0\)
hay BH=9(cm)
\(\Leftrightarrow AC=20cm\)
hay AH=12cm
10 tháng 9 2021
Ta có: \(AB^2=HB\cdot HC\)
\(\Leftrightarrow HB\left(HB+16\right)=225\)
\(\Leftrightarrow HB^2+16HB-225=0\)
\(\Leftrightarrow HB=9\left(cm\right)\)
\(\Leftrightarrow AC=\sqrt{HC\cdot BC}=\sqrt{16\cdot25}=20\left(cm\right)\)
\(\Leftrightarrow AH=12\left(cm\right)\)
GH
19 tháng 6 2023
Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\) (đl pytago)
\(\Leftrightarrow4a^2=a^2+AC^2\\\Rightarrow AC=4a^2-a^2=3a^2 \)
Vậy \(AC=\sqrt{3}a\)
Tam giác ABC vuông tại A có AH \(\perp\) AC tại H
Ta có:
\(BC.AH=AB.AC\) (hệ thức lượng)
\(\Leftrightarrow2a.AH=a.\sqrt{3}a\\ \Rightarrow AH=\dfrac{\sqrt{3}a^2}{2a}=\dfrac{\sqrt{3}a}{2}\)
Vậy \(AH=\dfrac{\sqrt{3}a}{2}\)
11 tháng 9 2021
\(AH=\dfrac{2\cdot AB}{BC}=\dfrac{2\cdot2\sqrt{2}}{4}=\sqrt{2}\left(cm\right)\)
\(BH=CH=\sqrt{AB^2-AH^2}=\sqrt{8-2}=\sqrt{6}\left(cm\right)\)