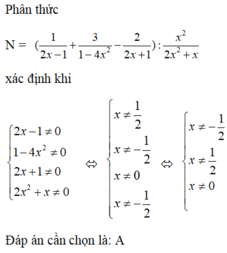\(\sqrt{\frac{-83}{376-22x}}\) xác định khi nào
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
17 tháng 9 2021
a, Hàm số xác định khi: \(\left\{{}\begin{matrix}cos\dfrac{x}{2}\ne3\\tanx\ne\sqrt{3}\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{3}+k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
BT
2
29 tháng 8 2019
ĐK: sin^2 (2x) ≥ 0 <=> sin 2x ≥ 0 <=> x ≥ kπ/2
=> HSXĐ <=> 1 + cot^2 (2x) ≥ 0
<=> cot^2 (2x) ≥ -1
<=> cot 2x = 0
<=> x = π/2 + k2π
PV
2
18 tháng 8 2017
Biểu thức xác định khi\(\hept{\begin{cases}\frac{x-2}{x^2-7x+12}\ge0\\x^2-7x+12\ne0\end{cases}}\)Từ đó bạn giải hệ phương trình này ra là sẽ ra đc điều kiện nha bn!
18 tháng 8 2017
\(\sqrt{\frac{x-2}{x^2-7x+12}}\)xác định
\(\Leftrightarrow\hept{\begin{cases}x-2\ge0\\x^2-7x+12\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge2\\x^2-3x-4x+12\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge2\\x\left(x-3\right)-4\left(x-3\right)\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge2\\\left(x-3\right)\left(x-4\right)\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge2\\x\ne3\\x\ne4\end{cases}}\)
vậy để phân thức xác định thì \(\hept{\begin{cases}x\ge2\\x\ne3\\x\ne4\end{cases}}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 6 2021
1.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx}{cosx}-sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
2.
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
3.
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\cos\left(x-\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{2}\right)\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
BN
2
12 tháng 12 2020
\(\sqrt{\dfrac{4-2x}{x^2}}\) có nghĩa thì \(\left\{{}\begin{matrix}4-2x\ge0\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x\le4\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le2\\x\ne0\end{matrix}\right.\)
BN
1
14 tháng 10 2021
\(ĐK:\dfrac{1}{x^2}\ge0\left(luôn.đúng.do.1>0;x^2>0\right);x\ne0\\ \LeftrightarrowĐK:x\in R;x\ne0\)
PT
1
CM
15 tháng 7 2019
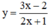có nghĩa khi 2x + 1 ≠ 0 ⇔ x ⇔ –1/2.
Vậy tập xác định của hàm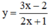 
là D = R \ {-1/2}.