Chứng minh rằng hai số sau là hai số nguyên tố cùng nhau3n+7và 4n+9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SN
1
12 tháng 11 2017
Gọi d là Ước chung lớn nhất của 5n+9 và 4n+7
=> 5n+9 chia hết cho d
4n+7 chia hết cho d
=> 4( 5n + 9 ) - 5( 4n + 7 ) chia hết cho d
=> ( 20n + 36 ) - ( 20n + 35 ) chia hết cho d
=> 1 chia hết cho d
=> d = 1
Vậy 5n+9 và 4n+7 là hai số nguyên tố cùng nhau
PT
1
CM
28 tháng 7 2017
Giả sử ƯCLN(2n+3 ;4n+8) = d
2 n + 3 ⋮ d 4 n + 8 ⋮ d ⇒ 2 2 n + 3 ⋮ d
=> 4 n + 8 - 2 2 n + 3 = 2 ⋮ d
=>d = 1 hoặc d = 2 .
Giả sử nếu d = 2 => (2n+3) ⋮ 2 (vô lý)
Vậy d = 1 hay 2n+3 và 4n+8 là hai số nguyên tố cùng nhau
PT
1
13 tháng 12 2021
Giả sử: \(UCLN\left(2n+3;4n+8\right)=d\)
=> \(\left\{{}\begin{matrix}2n+3⋮d\\4n+8⋮d\end{matrix}\right.\) => \(\left\{{}\begin{matrix}4n+6⋮d\\4n+8⋮d\end{matrix}\right.\)
=> \(2⋮d\) => \(\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)
Có 2n+3 là số lẻ => \(2n+3⋮̸2\)
=> d = 1
=> đpcm
HL
1
16 tháng 5 2023
Gọi d=ƯCLN(2n+5;4n+8)
=>4n+10-4n-8 chia hết cho d
=>2 chia hết cho d
mà 2n+5 lẻ
nên d=1
=>ĐPCM
PM
1
23 tháng 11 2016
Gọi \(ƯCLN\left(5n+9,4n+7\right)\) là d
\(\Rightarrow\begin{cases}5n+9⋮d\\4n+7⋮d\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}4\left(5n+9\right)⋮d\\5\left(4n+7\right)⋮d\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}20n+36⋮d\\20n+35⋮d\end{cases}\)
\(\Rightarrow\left(20n+36\right)-\left(20n+35\right)⋮d\)
\(\Rightarrow\left(20n+36-20n-35\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vì : \(d=1\Rightarrow\) 5n +9 và 4n + 7 là hai số nguyên tố cùng nhau
Vậy ...
NM
Nguyễn Minh Quang
Giáo viên
23 tháng 11 2020
gọi a là ước chung lớn nhất của 2n+1 và 3n+2
do đó a phải là ước của \(2\left(3n+2\right)-3\left(2n+1\right)=1\) do đó a=1
hay 2n+1 và 3n+2 là hai số nguyên tố cùng nhau.
b.gọi b là ước chung lớn nhất của 2n+3 và 4n+5
do đó b phải là ước của \(2\left(2n+3\right)-\left(4n+5\right)=1\)do đó b=1
hay 2n+3 và 4n+5 là hai số nguyên tố cùng nhau
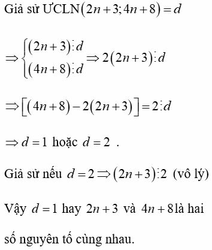
Gọi d là ƯC(3n+7;4n+9)
=> 3n+7 chia hết cho d (trong bài bạn ghi kí hiệu nha) =>4 .(3n+7) chia hết cho d =>12n+28 chia hết cho d
4n+9 chia hết cho d =>3.(4n+9) chia hết cho d=>12n+27 chia hết cho d
=> (12n+28-12n+27) chia hết cho d
1 chia hết cho d=> d=1
Kết luận:3m+7 và 4n+9 là hai số nguyên tố cùng nhau.(xong rùi bạn)