Giải Phương trình
(x2-3)3-(4x+6)3+216=18.(4x+6).(3-x2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
ĐKXĐ: $x\geq \frac{-3}{2}$
PT $\Leftrightarrow x^2-4x+21-6\sqrt{2x+3}=0$
$\Leftrightarrow (x^2-6x+9)+[(2x+3)-6\sqrt{2x+3}+9]=0$
$\Leftrightarrow (x-3)^2+(\sqrt{2x+3}-3)^2=0$
Ta thấy: $(x-3)^2\geq 0; (\sqrt{2x+3}-3)^2\geq 0$ với mọi $x\geq \frac{-3}{2}$
Do đó để tổng của chúng bằng $0$ thì:
$(x-3)^2=(\sqrt{2x+3}-3)^2=0$
$\Leftrightarrow x=3$ (tm)

1) `x^2+4-2(x-1)=(x-2)^2`
`<=>x^2+4-2x+2=x^2-4x+4`
`<=>-2x+2=-4x`
`<=>2x=-2`
`<=>x=-1`
.
2) ĐKXĐ: `x \ne \pm 3`
`(x+3)/(x-3)-(x-1)/(x+3)=(x^2+4x+6)/(x^2-9)`
`<=>(x+3)^2-(x-1)(x-3)=x^2+4x+6`
`<=>x^2+6x+9-x^2+4x-3=x^2+4x+6`
`<=>10x+6=x^2+4x+6`
`<=>x^2-6x=0`
`<=>x(x-6)=0`
`<=>x=0;x=6`
.
3) ĐKXĐ: `x \ne \pm 3`
`(3x-3)/(x^2-9) -1/(x-3 )= (x+1)/(x+3)`
`<=>(3x-3)-(x+3)=(x+1)(x-3)`
`<=> 2x-6=x^2-2x-3`
`<=>x^2-4x+3=0`
`<=>x^2-x-3x+3=0`
`<=>x(x-1)-3(x-1)=0`
`<=>(x-3)(x-1)=0`
`<=> x=3;x=1`
Vậy...

- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = x + 3 ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = 1; x2 = 3
x1 có thỏa mãn điều kiện nói trên
x2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1

- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = x + 3 ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = 1 ; x 2 = 3
x 1 có thỏa mãn điều kiện nói trên
x 2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1

Ta có: 3 x 3 +6 x 2 -4x =0 ⇔ x(3 x 2 +6x -4) =0
⇔ x = 0 hoặc 3 x 2 +6x -4 =0
Giải phương trình 3 x 2 +6x -4 =0
∆ ’ = 3 2 - 3(-4) = 9 + 12 = 21 > 0
∆ ' = 21
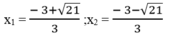
Vậy phương trình đã cho có 3 nghiệm
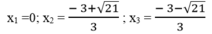
giải các Phương trình sau
a) (5x+3)(x2+1)(x-1)=0
b) (4x-1)(x-3)-(x-3)(5x+2)=0
c) (x+6)(3x-1)+x2-36 =0

a: =>(5x+3)(x-1)=0
=>x=1 hoặc x=-3/5
b: =>(x-3)(4x-1-5x-2)=0
=>(x-3)(-x-3)=0
=>x=-3 hoặc x=3
c: =>(x+6)(3x-1+x-6)=0
=>(x+6)(4x-7)=0
=>x=7/4 hoặc x=-6

`a,x^2 +4x-5=0`
`<=> x^2-x+5x-5=0`
`<=> x(x-1)+5(x-1)=0`
`<=>(x-1)(x+5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
`b, x^2 -x-12=0`
`<=> x^2 +3x-4x-12=0`
`<=>(x^2+3x)-(4x+12)=0`
`<=>x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`c, (2x-7)^2 - 6(2x-7)(x-3)=0`
`<=>(2x-7)(2x-7 -6x+18)=0`
`<=>(2x-7) ( -4x+11)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\-4x+11=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=7\\-4x=-11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=\dfrac{11}{4}\end{matrix}\right.\)
a: =>(x+5)(x-1)=0
=>x=1 hoặc x=-5
b: =>(x-4)(x+3)=0
=>x=4 hoặc x=-3
c: =>(2x-7)(2x-7-6x+18)=0
=>(2x-7)(-4x+11)=0
=>x=11/4 hoặc x=7/2

Bổ đề a^3+b^3+c^3-3abc= 0
<=> (a+b+c)[a^2+b^2+c^2-ab-bc-ca]=0
<=> 1/2 .(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]=0
<=> a+b+c=0 hoặc a=b=c
Đặt u =x^2-3 , v= - (4x+6 )
Ta có u^3+v^3 +216 = 18.u.v
<=> u^3+v^3+6^3 - 3.6.uv=0
Áp dụng bổ đề
=> u=v=3 hoặc u+v+3=0
*TH1: u=v=3 => x^2-3=3 và 4x+6=-3 ( vô lý)
*TH2 : u+v+3=0 <=> x^2-3-(4x+6)+3=0 <=> x^2-4x-6=0
=> x=2+√10 hay x=2-√10